题目内容
1.总质量为M的火箭以速度v0飞行,质量为m的燃料相对于火箭以速率u向后喷出,则火箭的速度大小为( )| A. | V0+$\frac{m}{M}$u | B. | V0-$\frac{m}{M}$u | C. | V0+$\frac{m}{M-m}$(V0+u) | D. | V0+$\frac{m}{M-m}$u |
分析 对火箭和气体系统为研究对象,在水平方向上运用动量守恒定律,求出喷气后火箭相对于地面的速度.
解答 解:以火箭飞行的方向为正方向,以地面为参考系,
火箭被飞机释放后火箭喷出燃气前后瞬间,
设火箭的速度为v,则气体的速度:v′=v-u,
据动量守恒定律得:Mv0=(M-m)v+m(v-u),
解得:vx=v0+$\frac{m}{M}$u;
故选:A.
点评 解决本题的关键知道系统在水平方向上动量守恒,结合动量守恒进行求解,注意正方向的规定.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
11.一起重机的钢绳由静止开始匀加速提起质量为m的重物,当重物的速度为v1时,起重机的有用功率达到最大值P,以后起重机保持该功率不变,继续提升重物,直到以最大速度v2匀速上升为止,物体上升的高度为h,则整个过程中,下列说法正确的是( )
| A. | 钢绳的最大拉力为$\frac{P}{{v}_{2}}$ | B. | 钢绳的最大拉力小于$\frac{P}{{v}_{1}}$ | ||
| C. | 重物的最大速度v2=$\frac{P}{mg}$ | D. | 重物匀加速运动的加速度为$\frac{P}{m{v}_{1}}$ |
9.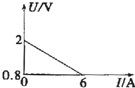 为研究问题方便,有时我们会把路端电压与干路电流的变化关系图象中I轴向上平移,使得图线“很快”便与I轴出现交点,如图所示.则由该图象可知( )
为研究问题方便,有时我们会把路端电压与干路电流的变化关系图象中I轴向上平移,使得图线“很快”便与I轴出现交点,如图所示.则由该图象可知( )
 为研究问题方便,有时我们会把路端电压与干路电流的变化关系图象中I轴向上平移,使得图线“很快”便与I轴出现交点,如图所示.则由该图象可知( )
为研究问题方便,有时我们会把路端电压与干路电流的变化关系图象中I轴向上平移,使得图线“很快”便与I轴出现交点,如图所示.则由该图象可知( )| A. | 电源电动势为2V | |
| B. | 电源内阻为$\frac{1}{3}$Ω | |
| C. | 电源的短路电流为6A | |
| D. | 电路路端电压为1V时,电路中的电流为5A |
16. 如图所示电路中,电池均相同,当电键S分别置于a、b两处时,导致MM′与NN′之间的安培力的大小分别为Fa、Fb,可判断这两段导线( )
如图所示电路中,电池均相同,当电键S分别置于a、b两处时,导致MM′与NN′之间的安培力的大小分别为Fa、Fb,可判断这两段导线( )
 如图所示电路中,电池均相同,当电键S分别置于a、b两处时,导致MM′与NN′之间的安培力的大小分别为Fa、Fb,可判断这两段导线( )
如图所示电路中,电池均相同,当电键S分别置于a、b两处时,导致MM′与NN′之间的安培力的大小分别为Fa、Fb,可判断这两段导线( )| A. | 电键S置于a时MM′与NN′之间相互吸引,且Fa>Fb | |
| B. | 电键S置于a时MM′与NN′之间相互吸引,且Fa<Fb | |
| C. | 电键S置于b时MM′与NN′之间相互排斥,且Fa>Fb | |
| D. | 电键S置于b时MM′与NN′之间相互排斥,且Fa<Fb |
13.小明用如图所示的装置探究加速度与力、质量的关系,实验中不需要的操作是( )
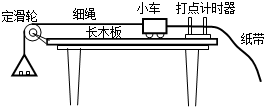

| A. | 先接通电源,后释放小车 | |
| B. | 调节定滑轮的高度,使细绳与长木板平行 | |
| C. | 用秒表测出小车运动的时间 | |
| D. | 将长木板右端垫高,平衡小车和纸带受到的摩擦力 |
 如图所示,某一真空室内充满竖直向下的匀强电场E,在竖直平面内建立坐标系xOy,在y<0的空间里有与场强E垂直的匀强磁场B,在y>0的空间内,将一质量为m的带电液滴(可视为质点)自由释放,此液滴则沿y轴的负方向,以加速度a=2g(g为重力加速度)做匀加速直线运动,当液滴运动到坐标原点时,被安置在原点的一个装置瞬间改变了带电性质(液滴所带电荷量和质量均不变),随后液滴进入y<0的空间运动.液滴在y<0的空间内的运动过程中( )
如图所示,某一真空室内充满竖直向下的匀强电场E,在竖直平面内建立坐标系xOy,在y<0的空间里有与场强E垂直的匀强磁场B,在y>0的空间内,将一质量为m的带电液滴(可视为质点)自由释放,此液滴则沿y轴的负方向,以加速度a=2g(g为重力加速度)做匀加速直线运动,当液滴运动到坐标原点时,被安置在原点的一个装置瞬间改变了带电性质(液滴所带电荷量和质量均不变),随后液滴进入y<0的空间运动.液滴在y<0的空间内的运动过程中( )