题目内容
17. 如图所示,圆形匀强磁场半径R=4cm,磁感应强度B2=10-2T,方向垂直纸面向外,其上方有一对水平放置的平行金属板M、N,间距为d=2cm,N板中央开有小孔S.小孔位于圆心O的正上方,S与O的连线交磁场边界于A.$\overline{SA}$=2cm,两金属板通过导线与宽度为L1=0.5m的金属导轨相连,导轨处在垂直纸面向里的匀强磁场中,磁感应强度为B1=1T.有一长为L2=1m的导体棒放在导轨上,导体棒与导轨接触良好且始终与导轨垂直.现对导体棒施一力F,使导体棒以v1=8m/s匀速向右运动.有一比荷$\frac{q}{m}$=5×107C/kg的粒子(不计重力)从M板处由静止释放,经过小孔S,沿SA进入圆形磁场,求:
如图所示,圆形匀强磁场半径R=4cm,磁感应强度B2=10-2T,方向垂直纸面向外,其上方有一对水平放置的平行金属板M、N,间距为d=2cm,N板中央开有小孔S.小孔位于圆心O的正上方,S与O的连线交磁场边界于A.$\overline{SA}$=2cm,两金属板通过导线与宽度为L1=0.5m的金属导轨相连,导轨处在垂直纸面向里的匀强磁场中,磁感应强度为B1=1T.有一长为L2=1m的导体棒放在导轨上,导体棒与导轨接触良好且始终与导轨垂直.现对导体棒施一力F,使导体棒以v1=8m/s匀速向右运动.有一比荷$\frac{q}{m}$=5×107C/kg的粒子(不计重力)从M板处由静止释放,经过小孔S,沿SA进入圆形磁场,求:(1)导体棒两端的电压;
(2)M、N之间场强的大小和方向;
(3)粒子在离开磁场前运动的总时间(计算时取π=3).
分析 (1)根据公式E=BLv求出导体棒两端的电压;
(2)结合上题的结果求出M、N之间的电压,根据匀强电场的电场强度公式E=$\frac{U}{d}$,求出M、N之间场强的大小和方向;
(3)带电粒子在电场中加速,再在磁场中偏转,根据牛顿第二定律和运动学公式求出在电场中运动的时间.根据带电粒子在磁场中运动的周期公式和圆心角的大小,求出粒子在磁场中的运动的时间,从而得出离子在磁场中运动的总时间.
解答 解:(1)导体棒两端的电压为:U1=E2=B2L2v1=1×1×8V=8V.
(2)M、N之间的电压为:U2=E2=B2L1v1=1×0.5×8V=4V.
M、N之间的场强大小 E=$\frac{{U}_{2}}{d}$=$\frac{4}{0.02}$=200V/m,方向竖直向下.
(3)粒子在MN间加速运动的过程,有:a=$\frac{qE}{m}$=5×107×200=1×1010m/s2;
由 d=$\frac{1}{2}$a${t}_{1}^{2}$得:t1=$\sqrt{\frac{2d}{a}}$=$\sqrt{\frac{2×2×1{0}^{-2}}{1×1{0}^{10}}}$s=2×10-6s,
粒子离开电场时的速度为:v=at1=1×1010×2×10-6=2×104m/s,
粒子在SA段运动的时间为:t2=$\frac{\overline{SA}}{v}$=$\frac{2×1{0}^{-2}}{2×1{0}^{4}}$=1×10-6s,
粒子在匀强磁场中做匀速圆周运动.有:qvB1=m$\frac{{v}^{2}}{r}$,
解得:r=$\frac{mv}{q{B}_{1}}$=$\frac{2×1{0}^{4}}{5×1{0}^{7}×1×1{0}^{-2}}$m=0.04m=4cm,
则知得:r=d
设粒子在磁场轨迹对应的圆心角为θ,则由几何知识得:θ=90°
则粒子在磁场中运动的时间为:t3=$\frac{1}{4}$T=$\frac{1}{4}$•$\frac{2πm}{q{B}_{1}}$=$\frac{1}{2}$×$\frac{3}{5×1{0}^{7}×1×1{0}^{-2}}$s=3×10-6s,
故粒子在离开磁场前运动的总时间 t=t1+t2+t3=(2+1+3)×10-6 s=6×10-6s.
答:(1)导体棒两端的电压是8V;
(2)M、N之间的电场强度的大小200V/m,方向竖直向下;
(3)粒子在离开磁场前运动的总时间是6×10-6 s.
点评 解决本题的关键掌握法拉第电磁感应定律,掌握带电粒子在匀强磁场中运动的半径公式和周期公式,结合几何关系进行求解.

| A. | 月球绕地球运行的周期及月地距离 | |
| B. | 月球绕地球运行的速度和地球的质量 | |
| C. | 月球半径登月舱在月面附近的绕行周期 | |
| D. | 月球半径及登月舱的质量 |
| A. | 跳过2.45m的高度时他的速度为零 | |
| B. | 起跳时地面对它的支持力不做功 | |
| C. | 起跳时地面对它的支持力大于他对地面的压力 | |
| D. | 起跳以后上升过程他处于完全失重状态 |
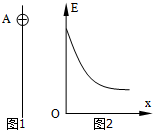 某空间区域有竖直方向的电场(图1中只画出了一条电场线),一个质量为m、电荷量为q的带正电的小球,在电场中从A点由静止开始沿电场线竖直向下运动,不计一切阻力,运动过程中物体的机械能E与物体位移x关系的图象如图2所示,由此可以判断( )
某空间区域有竖直方向的电场(图1中只画出了一条电场线),一个质量为m、电荷量为q的带正电的小球,在电场中从A点由静止开始沿电场线竖直向下运动,不计一切阻力,运动过程中物体的机械能E与物体位移x关系的图象如图2所示,由此可以判断( )| A. | 物体所处的电场为非匀强电场,且场强不断减小,场强方向向上 | |
| B. | 物体所处的电场为匀强电场,场强方向向下 | |
| C. | 物体可能先做加速运动,后做匀速运动 | |
| D. | 物体一定做加速运动,且加速度不断减小 |
| A. | 140s | B. | 105s | C. | 84s | D. | 60$\sqrt{7}$s |
 如图所示,闭合电建S,理想电压表的示数为U,电流表的示数为I,现向左移动触头P,电压表V的示数改变量的大小为△U,电流表的示数改变量大小为△I,则下列说法正确的是( )
如图所示,闭合电建S,理想电压表的示数为U,电流表的示数为I,现向左移动触头P,电压表V的示数改变量的大小为△U,电流表的示数改变量大小为△I,则下列说法正确的是( )| A. | $\frac{U}{I}$变大 | B. | $\frac{△U}{△I}$=R2+r | ||
| C. | 电阻R1的功率变大 | D. | 电源的总功率变大 |
| A. | 刹车时的初速度越大,车的惯性一定越大 | |
| B. | 刹车所用的时间越长,表明车的惯性一定越大 | |
| C. | 刹车线越长,表明车的惯性一定越大 | |
| D. | 汽车满载时的惯性一定比空载时大 |
 如图,倾角为θ=37°的斜面放在粗糙的水平面上,质量为m的物块恰好沿斜面以速度v匀速下滑,现给m施加一与竖直方向成37°的斜向上的拉力F,小物块能继续沿斜面下滑有,斜面仍静止,sin37°=0.6,cos37°=0.8,则( )
如图,倾角为θ=37°的斜面放在粗糙的水平面上,质量为m的物块恰好沿斜面以速度v匀速下滑,现给m施加一与竖直方向成37°的斜向上的拉力F,小物块能继续沿斜面下滑有,斜面仍静止,sin37°=0.6,cos37°=0.8,则( )| A. | 物块与斜面间的动摩擦因数为0.75 | |
| B. | 拉力F作用下小物块继续下滑过程中地面对斜面的摩擦力大小为0.6F | |
| C. | 拉力F作用下小物块继续下滑过程中地面对斜面的摩擦力大小为0 | |
| D. | 若水平面光滑,施加力F时,斜面将向右运动 |
 氢原子能级及各能级值如图所示.当大量氢原子从第4能级向第2能级跃迁时,可以释放出3种不同频率的光子,所释放的光子最小频率为$\frac{{E}_{4}-{E}_{3}}{h}$(用普朗克常量h和图中给出的能级值字母表示).
氢原子能级及各能级值如图所示.当大量氢原子从第4能级向第2能级跃迁时,可以释放出3种不同频率的光子,所释放的光子最小频率为$\frac{{E}_{4}-{E}_{3}}{h}$(用普朗克常量h和图中给出的能级值字母表示).