题目内容
4.一辆质量为m,额定功率为P的小车从静止开始以恒定的加速度a起动,所受阻力为f,经时间t,行驶距离l后达到最大速度vm,然后匀速运动,则从静止开始到最大速度过程中,机车牵引力所做的功为( )| A. | Pt | B. | (f+ma)l | C. | $\frac{1}{2}$mvm2 | D. | $\frac{1}{2}$mvm2+fl |
分析 小车以恒定加速度起动,实际功率不断增大,可根据牛顿第二定律求出牵引力,由功的计算公式求牵引力做功,也可以由动能定理可求出牵引力做功.
解答 解:A、小车以恒定加速度起动,牵引力不变,由P=Fv知,小车的实际功率不断增大,不能根据W=Pt求牵引力做的功.故A错误.
B、根据牛顿第二定律得:F-f=ma,得牵引力大小 F=f+ma,由于在此过程中牵引力是恒力,所以牵引力所做的功为 W=Fl=(f+ma)l,故B正确.
CD、由动能定理可知:W-fl=$\frac{1}{2}m{v}_{m}^{2}$,解得:牵引力做功 W=$\frac{1}{2}m{v}_{m}^{2}$+fl,故C错误,D正确.
故选:BD
点评 本题要明确牵引力是恒力时,有两种方向可求其做功:一种:功的计算公式.另一种:动能定理.不要漏解.

练习册系列答案
相关题目
14.一辆汽车以额定功率在水平公路上沿直线行驶,经过3min,速度由36km/h提高到72km/h,则在这段时间内,汽车驶过的路程为( )
| A. | 一定小于2.7km | B. | 可能大于3.6km | ||
| C. | 一定大于2.7km,小于3.6km | D. | 以上情况均可能 |
19.下列物体运动的速度哪个大( )
| A. | 发射人造卫星的最起码速度:7.9km/s | |
| B. | 炮弹:100m/s | |
| C. | 蜗牛:1.5mm/s | |
| D. | 火车:360km/h |
9.下列说法正确的是( )
| A. | 具有各向异性的固定一定是晶体 | |
| B. | 悬浮在液体中的小颗粒越大,布朗运动越剧烈 | |
| C. | 露珠呈球状是由于液体表面张力的作用 | |
| D. | 两个分子间的引力或斥力均随分子间距的增大而减小,但斥力比引力减小得更快 | |
| E. | 把两块纯净的铅压紧,它们会“粘”在一起,说明分子间只存在分子引力 |
16.下列物理量属于矢量的是( )
| A. | 电场强度E | B. | 电流强度I | C. | 功率P | D. | 周期T |
10. 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )
如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )
 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )
如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )| A. | 球的速度v等于L$\sqrt{\frac{g}{2H}}$ | |
| B. | 球从击球点至落地点的动能减少了$\frac{1}{2}$mv2 | |
| C. | 球从击球点至落地点的重力势能减少了mgH | |
| D. | 球从击球点至落地点的机械能减少了mgH+$\frac{1}{2}$mv2 |
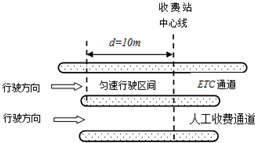 我国ETC联网正式启动运行,ETC是电子不停车收费系统的简称.汽车分别通过ETC通道和人工收费通道的流程如图所示.假设汽车以v1=15m/s朝收费站正常沿直线行驶,如果通过ETC通道,需要在收费站中心线前l0m处正好匀减速至v2=5m/s,匀速通过中心线后,再匀加速至v1正常行驶;如果通过人工收费通道,需要匀减速至中心线处停下,经过15s缴费成功后,再启动汽车匀加速至v1正常行驶.设汽车加速和减速过程中的加速度大小均为l m/s2.求:
我国ETC联网正式启动运行,ETC是电子不停车收费系统的简称.汽车分别通过ETC通道和人工收费通道的流程如图所示.假设汽车以v1=15m/s朝收费站正常沿直线行驶,如果通过ETC通道,需要在收费站中心线前l0m处正好匀减速至v2=5m/s,匀速通过中心线后,再匀加速至v1正常行驶;如果通过人工收费通道,需要匀减速至中心线处停下,经过15s缴费成功后,再启动汽车匀加速至v1正常行驶.设汽车加速和减速过程中的加速度大小均为l m/s2.求: 如图,足够长的平行玻璃砖厚度d=6cm,底面镀有反光膜,顶面嵌有涂有遮光物质的挡板AB,一束光线以i=60°的入射角由挡板的A端射入玻璃砖,经底面反射后,恰能从挡板的B端射出,不考虑光在玻璃砖上表面的反射.已知光线在玻璃砖中的折射率n=$\sqrt{3}$,真空中的光速c=3×108m/s,求:
如图,足够长的平行玻璃砖厚度d=6cm,底面镀有反光膜,顶面嵌有涂有遮光物质的挡板AB,一束光线以i=60°的入射角由挡板的A端射入玻璃砖,经底面反射后,恰能从挡板的B端射出,不考虑光在玻璃砖上表面的反射.已知光线在玻璃砖中的折射率n=$\sqrt{3}$,真空中的光速c=3×108m/s,求: