题目内容
14．
（多选）如图，一长为L的轻质细杆一端与质量为m的小球（可视为质点）相连，另一端可绕O点转动，现使轻杆在同一竖直面内作匀速转动，测得小球的向心加速度大小为g（g为当地的重力加速度），下列说法正确的是（ ）| A． | 小球的线速度大小为gL | |
| B． | 小球运动到最高点时处于完全失重状态 | |
| C． | 当轻杆转到水平位置时，轻杆对小球作用力方向斜向上与半径成45°角 | |
| D． | 轻杆在匀速转动过程中，轻杆对小球作用力的最大值为mg |
分析 根据a=$\frac{{v}^{2}}{r}$求解线速度，小球在最高点的加速度为g，处于完全失重状态，匀速圆周运动合外力提供向心力，在最低点对小球的作用力最大，根据向心力公式列式即可求解最大值．
解答 解：A、根据a=$\frac{{v}^{2}}{r}$=g得：v=$\sqrt{gL}$，故A正确；
B、小球做匀速圆周运动，加速度为g，所以小球在最高点的加速度为g，处于完全失重状态，故B正确；
C、当轻杆转到水平位置时，杆子和重力的合力指向圆心，合力为mg，重力为mg，所以轻杆对小球作用力方向斜向上与半径成45°角，故C正确；
D、在最低点杆子对小球的作用力最大，即F-mg=ma，解得F=2mg，故D错误．
故选：BC
点评 本题主要考查了向心力公式的直接应用，知道匀速圆周运动合外力提供向心力，物体的加速度为g时处于完全失重状态，难度不大，属于基础题．
练习册系列答案
相关题目
4．
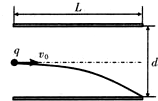如图所示，两平行金属板水平放置，板长为L，板间距离为d板间电压为U，一不计重力电荷量为q带电粒子以初速度v0沿两板的中线射入，恰好沿下板的边缘飞出，粒子通过平行金属板的时间为t，则（ ）
如图所示，两平行金属板水平放置，板长为L，板间距离为d板间电压为U，一不计重力电荷量为q带电粒子以初速度v0沿两板的中线射入，恰好沿下板的边缘飞出，粒子通过平行金属板的时间为t，则（ ）| A． | 在前$\frac{t}{2}$时间内，电场力对粒子做的功为$\frac{1}{4}$Uq | |
| B． | 在后$\frac{t}{2}$时间内，电场力对粒子做的功为$\frac{3}{8}$Uq | |
| C． | 在粒子下落的前$\frac{d}{4}$和后$\frac{d}{4}$过程中，电场力做功之比为2：1 | |
| D． | 在粒子下落的前$\frac{d}{4}$和后$\frac{d}{4}$过程中，电场力做功之比为1：2 |
5．
如图所示，一物体从圆弧形轨道的A点无初速滑下，物体与圆弧轨道间的动摩擦因数为μ，由于摩擦力的作用物体沿轨道到达C点时的速度为零，C点比A点下降了h1，物体又由C点沿轨道滑至B点，速度再次为零，B比C下降了h2，则h1与h2比较有（ ）
如图所示，一物体从圆弧形轨道的A点无初速滑下，物体与圆弧轨道间的动摩擦因数为μ，由于摩擦力的作用物体沿轨道到达C点时的速度为零，C点比A点下降了h1，物体又由C点沿轨道滑至B点，速度再次为零，B比C下降了h2，则h1与h2比较有（ ）| A． | h1＞h2 | B． | h1＜h2 | C． | h1=h2 | D． | 无法确定 |
2．（多选）人握住旗杆匀速上爬，则下列说法正确的是（ ）
| A． | 人受到的摩擦力的方向是沿杆向下的 | |
| B． | 人受到的摩擦力的方向是沿杆向上的 | |
| C． | 人握旗杆用力越大，人受的摩擦力也越大 | |
| D． | 人握旗杆用力越大，并不会使人受的摩擦力增大 |
如图所示为皮带传动装置，左轮O1是一个轮轴，大轮半径为R1，小轮半径为R2，A、B分别是大轮和小轮边缘上的点，右轮O2的半径为R3，C是右轮边缘上的点，已知R1：R2：R3=3：2：1，转动中皮带不打滑．
2．下列说法正确的是（ ）
| A． | 力和位移都是矢量，所以功也是矢量 | |
| B． | 正功大于负功 | |
| C． | 人能够搬动重物做功，说明人具有能量 | |
| D． | 机械效率高，表示机械做功快 |
如图所示为交流发电机示意图，匝数为n=100匝的矩形线圈，边长分别为10cm和20cm，内阻为5Ω，在磁感应强度B=0.5T的匀强磁场中绕OO′轴以50$\sqrt{2}$rad/s的角速度匀速转动，转动开始时线圈平面与磁场方向平行，线圈通过电刷和外部20Ω的电阻R相接．求电键S合上后，
如图所示，杆长为L，杆的一端固定一质量为m的小球，杆的质量忽略不计，整个系统绕杆的另一端O在竖直平面内作圆周运动，求：