题目内容
4.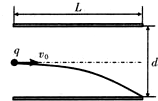 如图所示,两平行金属板水平放置,板长为L,板间距离为d板间电压为U,一不计重力电荷量为q带电粒子以初速度v0沿两板的中线射入,恰好沿下板的边缘飞出,粒子通过平行金属板的时间为t,则( )
如图所示,两平行金属板水平放置,板长为L,板间距离为d板间电压为U,一不计重力电荷量为q带电粒子以初速度v0沿两板的中线射入,恰好沿下板的边缘飞出,粒子通过平行金属板的时间为t,则( )| A. | 在前$\frac{t}{2}$时间内,电场力对粒子做的功为$\frac{1}{4}$Uq | |
| B. | 在后$\frac{t}{2}$时间内,电场力对粒子做的功为$\frac{3}{8}$Uq | |
| C. | 在粒子下落的前$\frac{d}{4}$和后$\frac{d}{4}$过程中,电场力做功之比为2:1 | |
| D. | 在粒子下落的前$\frac{d}{4}$和后$\frac{d}{4}$过程中,电场力做功之比为1:2 |
分析 带正电的粒子进入水平放置的平行金属板内,做类平抛运动,竖直方向做初速度为0的匀加速运动,由推论可求出在前$\frac{t}{2}$时间内和在后$\frac{t}{2}$时间内竖直位移之比,由动能定理求出电场力做功.粒子在下落前$\frac{d}{4}$和后$\frac{d}{4}$内,电场力做功相同.
解答 解:A、B、设粒子在前$\frac{t}{2}$时间内和在后$\frac{t}{2}$时间内竖直位移分别为y1、y2,由y=$\frac{1}{2}a{t}^{2}$和匀变速直线运动的推论可知y1:y2=1:3,
得:y1=$\frac{1}{8}$d,y2=$\frac{3}{8}$d,
则在前$\frac{t}{2}$时间内,电场力对粒子做的功为:W1=q•$\frac{1}{8}$U=$\frac{1}{8}$qU,
在后$\frac{t}{2}$时间内,电场力对粒子做的功为:W2=q•$\frac{3}{8}$U=$\frac{3}{8}$qU.故A错误,B正确;
C、D、根据W=qEy可得,在粒子下落前$\frac{d}{4}$和后$\frac{d}{4}$的过程中,电场力做功之比为1:1,故CD错误.
故选:B
点评 本题是类平抛运动,要熟练掌握其研究方法:运动的合成与分解,并要抓住竖直方向初速度为零的匀加速运动的一些推论,研究位移和时间关系.

练习册系列答案
相关题目
14. 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.( )
 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.( )| A. | 副线圈输出电压的频率为5Hz | |
| B. | 副线圈输出电压的有效值为22V | |
| C. | P向右移动时,原、副线圈的电流比减小 | |
| D. | P向右移动时,变压器的输出功率增加 |
15.下列说法正确的是 ( )
| A. | 入射光的强度变大时,打出光电子的初动能一定增大 | |
| B. | 放射性元素的半衰期与外界的温度无关 | |
| C. | 一个氢原子从n=3的激发态跃迁到基态时,能辐射三种不同频率的光子 | |
| D. | 卢瑟福依据少数α粒子发生大角度散射提出了原子核内质子的存在 | |
| E. | 按照波尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子总能量增大 |
19.如图所示,一物体以速度v0冲向光滑斜面AB,并能沿斜面升高h,下列说法正确的是( )


| A. | 若把斜面从C点锯断,由机械能守恒定律知,物体冲出C点后仍能升高h | |
| B. | 若把斜面弯成如图所示的半圆弧形,物体仍能沿AB升高h | |
| C. | 若把斜面从C点锯断或弯成如图所示的半圆弧状,物体都不能升高h,因为机械能不守恒 | |
| D. | 若把斜面从C点锯断或弯成如图所示的半圆弧状,物体都不能升高h,但机械能仍守恒 |
13. 如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )
如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )
 如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )
如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )| A. | 如果立即做匀加速运动,在绿灯熄灭前汽车能通过停车线 | |
| B. | 如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速 | |
| C. | 如果立即做匀减速运动,在绿灯熄灭前汽车不一定能通过停车线 | |
| D. | 如果距停车线5m处减速,汽车能停在停车线处 |
14. (多选)如图,一长为L的轻质细杆一端与质量为m的小球(可视为质点)相连,另一端可绕O点转动,现使轻杆在同一竖直面内作匀速转动,测得小球的向心加速度大小为g(g为当地的重力加速度),下列说法正确的是( )
(多选)如图,一长为L的轻质细杆一端与质量为m的小球(可视为质点)相连,另一端可绕O点转动,现使轻杆在同一竖直面内作匀速转动,测得小球的向心加速度大小为g(g为当地的重力加速度),下列说法正确的是( )
 (多选)如图,一长为L的轻质细杆一端与质量为m的小球(可视为质点)相连,另一端可绕O点转动,现使轻杆在同一竖直面内作匀速转动,测得小球的向心加速度大小为g(g为当地的重力加速度),下列说法正确的是( )
(多选)如图,一长为L的轻质细杆一端与质量为m的小球(可视为质点)相连,另一端可绕O点转动,现使轻杆在同一竖直面内作匀速转动,测得小球的向心加速度大小为g(g为当地的重力加速度),下列说法正确的是( )| A. | 小球的线速度大小为gL | |
| B. | 小球运动到最高点时处于完全失重状态 | |
| C. | 当轻杆转到水平位置时,轻杆对小球作用力方向斜向上与半径成45°角 | |
| D. | 轻杆在匀速转动过程中,轻杆对小球作用力的最大值为mg |
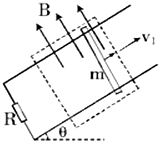 如图所示,平行的长直金属导轨倾斜放置,间距为L=2m、倾角为θ=37°,导轨下端接有阻值为R=2Ω的电阻,质量为m=0.2kg的导体棒垂直跨接在导轨上并保持静止.导轨和导体棒的电阻均不计,且接触良好.现导轨所在的平面上有一矩形区域内存在着垂直导轨平面向上的匀强磁场,磁感应强度大小为B=0.5T.开始时,导体棒静止于磁场区域的上端,当磁场以速度v1=5m/s匀速沿倾斜导轨向上移动时,导体棒随之开始运动后受到大小恒为f=1.2N的滑动摩擦阻力作用,当棒达到稳定速度时,导体棒仍处于磁场区域内,已知:sin37°=0.6,cos37°=0.8,g=10m/s2.则:
如图所示,平行的长直金属导轨倾斜放置,间距为L=2m、倾角为θ=37°,导轨下端接有阻值为R=2Ω的电阻,质量为m=0.2kg的导体棒垂直跨接在导轨上并保持静止.导轨和导体棒的电阻均不计,且接触良好.现导轨所在的平面上有一矩形区域内存在着垂直导轨平面向上的匀强磁场,磁感应强度大小为B=0.5T.开始时,导体棒静止于磁场区域的上端,当磁场以速度v1=5m/s匀速沿倾斜导轨向上移动时,导体棒随之开始运动后受到大小恒为f=1.2N的滑动摩擦阻力作用,当棒达到稳定速度时,导体棒仍处于磁场区域内,已知:sin37°=0.6,cos37°=0.8,g=10m/s2.则: 如图所示为某学校一套校内备用供电系统,由一台内阻为1Ω的发电机向全校22个教室(每个教室有“220V,40W”的白炽灯6盏)供电.如果输电线的总电阻R是4Ω,升压变压器和降压变压器(都认为是理想变压器)的匝数比分别是1:4和4:1,每个教室的白炽灯都正常发光,求:
如图所示为某学校一套校内备用供电系统,由一台内阻为1Ω的发电机向全校22个教室(每个教室有“220V,40W”的白炽灯6盏)供电.如果输电线的总电阻R是4Ω,升压变压器和降压变压器(都认为是理想变压器)的匝数比分别是1:4和4:1,每个教室的白炽灯都正常发光,求: