题目内容
7.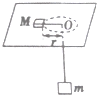 如图所示,细绳的一端系着质量为M=2kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5kg,M的中点与圆孔的距离为0.5m,并已知M与圆盘的最大静摩擦力为4N,现使此圆盘绕中心轴线转动,则物体的角速度ω取以下值可使m处于静止状态,(g取10m/s2)( )
如图所示,细绳的一端系着质量为M=2kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5kg,M的中点与圆孔的距离为0.5m,并已知M与圆盘的最大静摩擦力为4N,现使此圆盘绕中心轴线转动,则物体的角速度ω取以下值可使m处于静止状态,(g取10m/s2)( )| A. | ω=1.5 rad/s | B. | ω=2 rad/s | C. | ω=0.8 rad/s | D. | ω=3 rad/s |
分析 当此平面绕中心轴线以角速度ω转动时,若M恰好要向里滑动时,ω取得最小值,此时M所受的静摩擦力达到最大,方向沿半径向外,由最大静摩擦力和绳子拉力的合力提供M所需要的向心力.若M恰好要向外滑动时,ω取得最大值,此时M所受的静摩擦力达到最大,方向沿半径向里,由最大静摩擦力和绳子拉力的合力提供M所需要的向心力.根据牛顿第二定律分别求出ω的最小值和最大值,即可得到ω的取值范围.
解答 解:当物体M在此平面绕中心轴线以ω角速度转动时,当M恰好要向里滑动时,ω取得最小值为ωmin,此时M所受的静摩擦力达到最大为Fmax,方向沿半径向外,由最大静摩擦力和绳子拉力的合力提供所需要的向心力,根据牛顿第二定律和向心力公式有:mg-Fmax=Mωmin2r,代入数据解得ωmin=1 rad/s.
当M恰好要向外滑动时,ω取得最大值为ωmax,此时M所受的静摩擦力达到最大为Fmax,方向沿半径向里,由最大静摩擦力和绳子拉力的合力提供所需要的向心力,根据牛顿第二定律和向心力公式有:mg+Fmax=Mωmax2r,代入数据解得ωmax=3 rad/s.
所以角速度的取值范围是 1 rad/s≤ω≤3 rad/s,可使m处于静止状态,所以选项ABD正确,C错误.
故选:ABD
点评 本题是圆周运动中临界问题,抓住当M恰好相对此平面刚要滑动时静摩擦力达到最大,由牛顿第二定律求解角速度的取值范围

练习册系列答案
相关题目
16.关于路程和位移关系,下列说法中正确的是( )
| A. | 位移为零时,路程一定为零 | |
| B. | 路程一定大于位移 | |
| C. | 物体沿曲线运动时,位移的大小可能大于路程 | |
| D. | 物体沿直线单方向运动时,位移的大小一定等于路程 |
18.某实验小组用如图甲所示的电路测量一节蓄电池的电动势(约2V)和内阻,考虑蓄电池的内阻很小,电路中使用了一个保护电阻R0,除蓄电池、滑动变阻器R、开关、导线外,实验室中可供选用的器材还有:
A.电流表(量程3A,内阻约0.1Ω)
B.电压表(量程3V,内阻3kΩ)
C.电压表(量程1.8V,内阻1.8kΩ)
D.定值电阻(阻值1Ω,额定功率5W)
E.定值电阻(阻值5Ω,额定功率10W)

(1)实验时,电压表应该选用B,保护电阻应该选用D.(填器材前字母序号)
(2)在实验室进行仪器检查时发现电流表已经损坏不能用了,则下列实验改进方案中理论上可行的有ACD.
A.在缺少电流表的情况下,把滑动变阻器更换成电阻箱,来测蓄电池的电动势和内阻
B.按照实验电路图,在缺少电流表的情况下只依靠滑动变阻器调节,从而测出蓄电池的电动势和内阻
C.在缺少电流表的情况下,去掉滑动变阻器,只依靠更换保护电阻,测出两组数据,列式并联立求解蓄电池的电动势和内阻
D.在缺少电流表的情况下,用未使用的电压表与保护电阻并联,调节滑动变阻器测出多组数据,作图象求出蓄电池的电动势和内阻
(3)该实验小组经过讨论后,按照改进的电路图乙进行实验,调整滑动变阻器测得了5组两电压表的数据如表.
请在图丙中作出蓄电池的路端电压U1随保护电阻R0两端的电压U2变化的图象,并根据图象得出蓄电池的电动势E=2.05V,内阻r=0.10Ω.
A.电流表(量程3A,内阻约0.1Ω)
B.电压表(量程3V,内阻3kΩ)
C.电压表(量程1.8V,内阻1.8kΩ)
D.定值电阻(阻值1Ω,额定功率5W)
E.定值电阻(阻值5Ω,额定功率10W)

(1)实验时,电压表应该选用B,保护电阻应该选用D.(填器材前字母序号)
(2)在实验室进行仪器检查时发现电流表已经损坏不能用了,则下列实验改进方案中理论上可行的有ACD.
A.在缺少电流表的情况下,把滑动变阻器更换成电阻箱,来测蓄电池的电动势和内阻
B.按照实验电路图,在缺少电流表的情况下只依靠滑动变阻器调节,从而测出蓄电池的电动势和内阻
C.在缺少电流表的情况下,去掉滑动变阻器,只依靠更换保护电阻,测出两组数据,列式并联立求解蓄电池的电动势和内阻
D.在缺少电流表的情况下,用未使用的电压表与保护电阻并联,调节滑动变阻器测出多组数据,作图象求出蓄电池的电动势和内阻
(3)该实验小组经过讨论后,按照改进的电路图乙进行实验,调整滑动变阻器测得了5组两电压表的数据如表.
| 电压表V1读数U1(V) | 1.88 | 1.92 | 1.94 | 1.98 | 2.00 |
| 电压表V2读数U2(V) | 1.72 | 1.25 | 1.00 | 0.60 | 0.34 |
16.银河系的恒星中大约四分之一是双星,某双星由质量不等的星体S1和S2构成,两星在相互间的万有引力作用下绕两者连线上某一点C做匀速圆周运动.由天文观察测得其运行周期为T,S1到C点的距离为r1,S2的质量为m,已知引力常量为G,由此可求出两星间的距离r及两星的总质量M分别为( )
| A. | r=$\frac{T}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$ | B. | r=$\frac{T}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π{r}_{1}}\sqrt{\frac{Gm}{{r}_{1}}}$ | ||
| C. | r=$\frac{2π}{T}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$ | D. | r=$\frac{2π}{T}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π{r}_{1}}\sqrt{\frac{Gm}{{r}_{1}}}$ |
17.在平直道路上,甲汽车以速度v匀速行驶.当甲汽车司机发现前方距离为d处的乙汽车时,立即以大小为a1的加速度匀减速行驶,与此同时,乙汽车司机也发现了甲汽车,立即从静止开始以大小为a2的加速度沿甲汽车运动的方向匀加速运动,下列说法正确的是( )
| A. | 甲、乙两汽车之间的距离一定不断减小 | |
| B. | 甲、乙两汽车之间的距离可能先不断减小、后不断增大 | |
| C. | 若v>$\sqrt{2({a}_{1}+{a}_{2})d}$,则两汽车一定不会相撞 | |
| D. | 若v<$\sqrt{2({a}_{1}+{a}_{2})d}$,则两汽车一定不会相撞 |

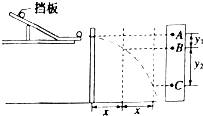 “研究平抛运动”的实验装置如图所示,实验步骤如下:
“研究平抛运动”的实验装置如图所示,实验步骤如下: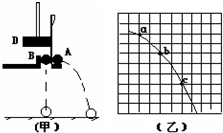 在“探究平抛运动的规律”的实验中,分成两步进行:
在“探究平抛运动的规律”的实验中,分成两步进行: