题目内容
16.银河系的恒星中大约四分之一是双星,某双星由质量不等的星体S1和S2构成,两星在相互间的万有引力作用下绕两者连线上某一点C做匀速圆周运动.由天文观察测得其运行周期为T,S1到C点的距离为r1,S2的质量为m,已知引力常量为G,由此可求出两星间的距离r及两星的总质量M分别为( )| A. | r=$\frac{T}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$ | B. | r=$\frac{T}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π{r}_{1}}\sqrt{\frac{Gm}{{r}_{1}}}$ | ||
| C. | r=$\frac{2π}{T}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$ | D. | r=$\frac{2π}{T}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π{r}_{1}}\sqrt{\frac{Gm}{{r}_{1}}}$ |
分析 这是一个双星的问题,S1和S2绕C做匀速圆周运动,它们之间的万有引力提供各自的向心力,S1和S2有相同的周期,结合牛顿第二定律和万有引力定律解决问题.
解答 解:根据万有引力提供向心力有:$G\frac{{m}_{1}m}{{r}^{2}}={m}_{1}{r}_{1}\frac{4{π}^{2}}{{T}^{2}}$;
整理得:r=$\frac{T}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$
又:$G\frac{{m}_{1}m}{{r}^{2}}=m{r}_{2}\frac{4{π}^{2}}{{T}^{2}}$
解得:m1=$\frac{m}{{r}_{1}}(r-{r}_{1})$.
则:M=m+m1=$\frac{mr}{{r}_{1}}$=$\frac{mT}{2π{r}_{1}}\sqrt{\frac{Gm}{{r}_{1}}}$.所以选项B正确.
故选:B
点评 该题属于双星问题,双星的特点是两个星体周期相等,星体间的万有引力提供各自所需的向心力.

练习册系列答案
相关题目
6. 如图所示,一光滑圆圈用细绳悬挂在天花板上.两个质量相同的小圆环从圈顶由静止开始同时向两边下滑.已知小圆环质量是圆圈质量的2倍.当细绳张力为零时,小圆环的位置对应的θ=( )
如图所示,一光滑圆圈用细绳悬挂在天花板上.两个质量相同的小圆环从圈顶由静止开始同时向两边下滑.已知小圆环质量是圆圈质量的2倍.当细绳张力为零时,小圆环的位置对应的θ=( )
 如图所示,一光滑圆圈用细绳悬挂在天花板上.两个质量相同的小圆环从圈顶由静止开始同时向两边下滑.已知小圆环质量是圆圈质量的2倍.当细绳张力为零时,小圆环的位置对应的θ=( )
如图所示,一光滑圆圈用细绳悬挂在天花板上.两个质量相同的小圆环从圈顶由静止开始同时向两边下滑.已知小圆环质量是圆圈质量的2倍.当细绳张力为零时,小圆环的位置对应的θ=( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
7.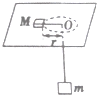 如图所示,细绳的一端系着质量为M=2kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5kg,M的中点与圆孔的距离为0.5m,并已知M与圆盘的最大静摩擦力为4N,现使此圆盘绕中心轴线转动,则物体的角速度ω取以下值可使m处于静止状态,(g取10m/s2)( )
如图所示,细绳的一端系着质量为M=2kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5kg,M的中点与圆孔的距离为0.5m,并已知M与圆盘的最大静摩擦力为4N,现使此圆盘绕中心轴线转动,则物体的角速度ω取以下值可使m处于静止状态,(g取10m/s2)( )
 如图所示,细绳的一端系着质量为M=2kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5kg,M的中点与圆孔的距离为0.5m,并已知M与圆盘的最大静摩擦力为4N,现使此圆盘绕中心轴线转动,则物体的角速度ω取以下值可使m处于静止状态,(g取10m/s2)( )
如图所示,细绳的一端系着质量为M=2kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5kg,M的中点与圆孔的距离为0.5m,并已知M与圆盘的最大静摩擦力为4N,现使此圆盘绕中心轴线转动,则物体的角速度ω取以下值可使m处于静止状态,(g取10m/s2)( )| A. | ω=1.5 rad/s | B. | ω=2 rad/s | C. | ω=0.8 rad/s | D. | ω=3 rad/s |
11.下列关于“验证力的平行四边形定则”实验中的注意事项,正确的是( )
| A. | 在同一次实验中,使橡皮条拉长时,结点O位置一定要相同 | |
| B. | 用两只弹簧测力计钩住绳套互成角度地拉橡皮条时,夹角应保持90° | |
| C. | 读数时应使细绳套与弹簧测力计的轴线在同一条直线上,避免弹簧测力计的外壳和弹簧测力计的限位孔之间有摩擦 | |
| D. | 在同一次实验中,画力的图示所选定的标度要相同 |
5. 一个带电粒子,沿垂直于磁场方向射入一匀强磁场,粒子的一段轨迹如图所示,a、b是轨迹上的两点.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(假设粒子所带电荷量不变,不计粒子的重力),则( )
一个带电粒子,沿垂直于磁场方向射入一匀强磁场,粒子的一段轨迹如图所示,a、b是轨迹上的两点.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(假设粒子所带电荷量不变,不计粒子的重力),则( )
 一个带电粒子,沿垂直于磁场方向射入一匀强磁场,粒子的一段轨迹如图所示,a、b是轨迹上的两点.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(假设粒子所带电荷量不变,不计粒子的重力),则( )
一个带电粒子,沿垂直于磁场方向射入一匀强磁场,粒子的一段轨迹如图所示,a、b是轨迹上的两点.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(假设粒子所带电荷量不变,不计粒子的重力),则( )| A. | 粒子带负电,从a向b运动 | B. | 粒子带正电,从a向b运动 | ||
| C. | 粒子带负电,从b向a运动 | D. | 粒子带正电,从b向a运动 |
 在“验证力的平行四边形定则”的实验中,用F1和F2两个力或用一个力F拉橡皮条时,结点必须达到同一点O,这是因为F1和F2共同作用时应与用一个力F作用时的作用效果相同.完成本实验时,以下几点:
在“验证力的平行四边形定则”的实验中,用F1和F2两个力或用一个力F拉橡皮条时,结点必须达到同一点O,这是因为F1和F2共同作用时应与用一个力F作用时的作用效果相同.完成本实验时,以下几点: 如图所示,在某次自由式滑雪比赛中,一运动员从弧形雪坡底部以大小为v0=10m/s的初速度沿水平方向飞出,最终落回到倾角为θ=37°的足够长斜面雪坡上.若运动员飞出后在空中的姿势保持不变,不计空气阻力的影响,重力加速度g取10m/s2,sin 37°=0.6,cos 37°=0.8.
如图所示,在某次自由式滑雪比赛中,一运动员从弧形雪坡底部以大小为v0=10m/s的初速度沿水平方向飞出,最终落回到倾角为θ=37°的足够长斜面雪坡上.若运动员飞出后在空中的姿势保持不变,不计空气阻力的影响,重力加速度g取10m/s2,sin 37°=0.6,cos 37°=0.8. 在《探究合力的求法》的实验中,两个弹簧秤的拉力F1和F2已于图中作出了它们的图示,O是橡皮条的一个端点,图中每格的长度代表1N.
在《探究合力的求法》的实验中,两个弹簧秤的拉力F1和F2已于图中作出了它们的图示,O是橡皮条的一个端点,图中每格的长度代表1N.