题目内容
18. 如图所示,AB是一段光滑的水平支持面,一个质量为m的小物体P在支持面上以速度v0滑到B点时水平飞出,落在水平地面的C点,其轨迹如图中虚线BC所示.已知P落地时相对于B点的水平位移OC=l,重力加速度为g,不记空气阻力的作用.
如图所示,AB是一段光滑的水平支持面,一个质量为m的小物体P在支持面上以速度v0滑到B点时水平飞出,落在水平地面的C点,其轨迹如图中虚线BC所示.已知P落地时相对于B点的水平位移OC=l,重力加速度为g,不记空气阻力的作用.(1)现于支持面下方紧贴B点安装一水平传送带,传送带右端E与B点相距$\frac{1}{2}$,先将驱动轮锁定,传送带处于静止状态.使P仍以v0离开B点在传送带上滑行,然后从传送带右端E水平飞出,恰好仍落在C点,其轨迹如图中虚线EC所示,求小物块P与传送带之间的动摩擦因数μ;
(2)若将驱动轮的锁定解除,并使驱动轮以角速度ω顺时针匀速转动,再使P仍以v0从B点滑上传送带,已知驱动轮的半径为r,传送带不打滑.若要使P最后仍落到C点,则求:
①驱动轮转动的角速度ω应该满足什么条件?
②在满足?的条件下,P与皮带间摩擦产生的热量Q
(3)若驱动轮以不同的角度ω顺时针匀速转动,仍使P以v0从B点滑上传送带,最后P的落地点为D(图中未画出).试写出角速度ω对应的OD的可能值.
分析 (1)小物体从B到C的过程与从E到C的过程,均做平抛运动,运动时间相等,根据水平位移关系求初速度关系,再对小物体从B到E的过程,由动能定理求动摩擦因数.
(2))①当传送带的速度 v=ωr≤vE,即ω≤$\frac{{v}_{0}}{2r}$时,物体在传送带上一直做匀减速运动,物体离开传送带时的速度为vE.
②在满足①的条件下,由运动学公式求出物体与传送带间的相对位移,再求热量Q.
(3)根据传送带速度范围,分析物体在传送带上的运动情况,得到物体离开传送带的速度,从而结合平抛运动的规律求得OD.
解答 解:(1)小物体从B到C的过程,做平抛运动,水平方向有 l=v0t0.
小物体从E到C的过程水平方向有 $\frac{l}{2}$=vEt0.
可得 vE=$\frac{{v}_{0}}{2}$
设小物体与传送带间的动摩擦因数为μ,小物体从B到E的过程,由动能定理得
-μmg$\frac{l}{2}$=$\frac{1}{2}m{v}_{E}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
解得 μ=$\frac{3{v}_{0}^{2}}{4gl}$
(2)①当传送带的速度 v=ωr≤vE,即ω≤$\frac{{v}_{0}}{2r}$时,物体在传送带上一直做匀减速运动,物体离开传送带时的速度为vE.
②在满足①的条件下,物体在传送带上做匀减速运动时间为t.
则有 $\frac{\frac{l}{2}}{t}$=$\frac{{v}_{0}+{v}_{E}}{2}$=$\frac{3{v}_{0}}{4}$
解得 t=$\frac{2l}{3{v}_{0}}$
此过程中,传送带通过的路程 S带=ωrt=$\frac{2ωrl}{3{v}_{0}}$
小物体与传送带间的相对位移 S相=$\frac{l}{2}$-S带=$\frac{l}{2}$-$\frac{2ωrl}{3{v}_{0}}$
所以P与皮带间摩擦产生的热量 Q=μmgS相=$\frac{3m{v}_{0}^{2}}{4}$($\frac{1}{2}$-$\frac{2ωr}{3{v}_{0}}$)
(3)(a)当传送带的速度满足 0<v带=ωr<vE,即 0<ω<$\frac{{v}_{0}}{2r}$时,物体在传送带上一直做匀减速运动,物体离开传送带时的速度为vE,则 OD=l.
(b)如果物体在传送带上一直做匀加速而未与传送带共速,则物体的加速度始终为 a=μg
物体离开传送带时的速度达到最大值为vmax.
根据运动学公式 vmax2-v02=2μg$\frac{l}{2}$
解得 vmax=$\frac{\sqrt{7}}{2}{v}_{0}$
当传送带的速度 v带=ωr≥$\frac{\sqrt{7}}{2}{v}_{0}$,即ω≥$\frac{\sqrt{7}{v}_{0}}{2r}$时,物体离开传送带时的速度为vmax.
则 OD=($\frac{1}{2}$+$\frac{\sqrt{7}}{2}$)l
(c)当传送带的速度 vE<v带=ωr<vmax,即$\frac{{v}_{0}}{2r}$<ω<$\frac{\sqrt{7}}{2}{v}_{0}$时
物体离开传送带时的速度为 v=v带=ωr,则 OD=($\frac{1}{2}$+$\frac{ωr}{{v}_{0}}$)l
答:
(1)小物块P与传送带之间的动摩擦因数μ是$\frac{3{v}_{0}^{2}}{4gl}$;
(2)①驱动轮转动的角速度ω应该满足ω≤$\frac{{v}_{0}}{2r}$的条件.
②在满足?的条件下,P与皮带间摩擦产生的热量Q为$\frac{3m{v}_{0}^{2}}{4}$($\frac{1}{2}$-$\frac{2ωr}{3{v}_{0}}$).
(3)(a)当 0<ω<$\frac{{v}_{0}}{2r}$时,OD为l.
(b)当ω≥$\frac{\sqrt{7}{v}_{0}}{2r}$时,OD为($\frac{1}{2}$+$\frac{\sqrt{7}}{2}$)l
(c)当$\frac{{v}_{0}}{2r}$<ω<$\frac{\sqrt{7}}{2}{v}_{0}$时OD为($\frac{1}{2}$+$\frac{ωr}{{v}_{0}}$)l.
点评 本题要具有分析物体运动过程的能力,要抓住平抛运动的时间由高度决定这一知识点,要注意摩擦产生的热量与相对位移有关.

 口算题天天练系列答案
口算题天天练系列答案| A. | 0.2 | B. | 0.3 | C. | 0.5 | D. | 0 |
| A. | 当r>r0时,引力大于斥力,r增大时分子力做负功,Ep增加 | |
| B. | 当分子间距r变小时,引力减小,斥力增大 | |
| C. | 当r<r0时,引力大于斥力,r减小时分子力做负功,Ep减小 | |
| D. | 当r=r0时,Ep=0 |
 如图所示,两个分子之间的距离为r,当r增大时,这两个分子之间的分子力( )
如图所示,两个分子之间的距离为r,当r增大时,这两个分子之间的分子力( )| A. | 一定增大 | B. | 一定减小 | C. | 可能增大 | D. | 可能减小 |

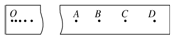 在“验证机械能守恒定律”的实验中,已知电磁打点计时器所用的电源的频率为50Hz,查得当地的重力加速度g=9.80m/s2,测得所用的重物质量为1.00kg.实验中得到一条点迹清晰的纸带(如图所示),把第一个点记作O,另选连续的四个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.99cm、70.18cm、77.76cm、85.73cm.
在“验证机械能守恒定律”的实验中,已知电磁打点计时器所用的电源的频率为50Hz,查得当地的重力加速度g=9.80m/s2,测得所用的重物质量为1.00kg.实验中得到一条点迹清晰的纸带(如图所示),把第一个点记作O,另选连续的四个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.99cm、70.18cm、77.76cm、85.73cm.