题目内容
18.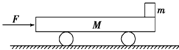 如图所示,质量M=2kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=6N,当小车向右运动的速度达到3m/s时,在小车前端轻轻地放上一个大小不计,质量为m=1kg的小物块,物块与小车间的动摩擦因数μ=0.4,小车足够长(取g=10m/s2).求:
如图所示,质量M=2kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=6N,当小车向右运动的速度达到3m/s时,在小车前端轻轻地放上一个大小不计,质量为m=1kg的小物块,物块与小车间的动摩擦因数μ=0.4,小车足够长(取g=10m/s2).求:(1)放上小物块瞬间,小物块与小车的加速度大小;
(2)经多长时间两者达到相同的速度;
(3)从小物块放上小车开始,经过t=2s小物块通过的位移大小.
分析 (1)根据牛顿第二定律分别求出物块和小车的加速度大小.
(2)根据速度时间公式求出物块和小车速度相等的时间;
(3)分析物体和车的运动的过程可以知道,车的运动可以分为两个过程,利用位移公式分别求得两个过程的位移,即可求得总位移的大小.
解答 解:(1)根据牛顿第二定律,
小物块的加速度为:am=$\frac{μmg}{m}$=μg=4m/s2
小车的加速度为:aM=$\frac{F-μmg}{M}$=$\frac{6-0.4×1×10}{2}$=1m/s2
(2)设经t时间两者达到相同的速度.由amt=v0+aMt代入数据得:t=1s
(3)在开始1s内小物块的位移为:
x1=$\frac{1}{2}$amt2=$\frac{1}{2}×4×{1}^{2}$m=2m
1s末物块的速度为:v=amt=4m/s
在接下来的1s小物块与小车相对静止,一起做加速运动且加速度为:
a=$\frac{F}{M+m}$=$\frac{6}{2+1}$=2m/s2
这1s内的位移为:x2=vt1+$\frac{1}{2}$at12=4×1+$\frac{1}{2}$×2×1=5m
则小物块通过的总位移为:x=x1+x2=7m
答:(1)放上小物块瞬间,小物块与小车的加速度大小分别为4m/s2和1m/s2;
(2)经1s时间两者达到相同的速度;
(3)从小物块放上小车开始,经过t=2s小物块通过的位移大小是7m.
点评 解决本题的关键理清物块和小车的运动规律,结合牛顿第二定律和运动学公式综合求解,要知道加速度是联系力和运动的纽带,在这类问题中是必未求的量.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
3.下列说法正确的是( )
| A. | 有加速度的物体其速度一定增加 | |
| B. | 物体的速度有变化,则一定有加速度 | |
| C. | 物体具有加速度,其速度可以是零 | |
| D. | 物体加速度减小时,速度一定减小 |
4.下列情况中的速度,属于平均速度的是( )
| A. | 子弹出枪口速度是800m/s | |
| B. | 汽车通过站牌时的速度是72km/h | |
| C. | 汽车从甲站开往乙站的速度是40km/h | |
| D. | 小球第3秒末的速度是6m/s |
13. 物体在与其初速度始终共线的合力F作用下运动,取v0的方向为正方向,合力F随时间t的变化情况如图所,则在0-t1这段时间内( )
物体在与其初速度始终共线的合力F作用下运动,取v0的方向为正方向,合力F随时间t的变化情况如图所,则在0-t1这段时间内( )
 物体在与其初速度始终共线的合力F作用下运动,取v0的方向为正方向,合力F随时间t的变化情况如图所,则在0-t1这段时间内( )
物体在与其初速度始终共线的合力F作用下运动,取v0的方向为正方向,合力F随时间t的变化情况如图所,则在0-t1这段时间内( )| A. | 物体的加速度先减小后增大,速度先减小后增大 | |
| B. | 物体的加速度线增大后减小,速度先增大后减小 | |
| C. | 物体的加速度线增大后减小,位移先增大后减小 | |
| D. | 物体的加速度先增大后减小,速度一直增大 |
10.在远距离输电时,输送的电功率为P,输电电压为U,输电电流为I,所用导线电阻率为ρ,横截面积为S,总长度为L,输电线损失的电功率为P损,用户得到的电功率为P用,则P损、P用的关系式正确的是( )
| A. | I=$\frac{P}{U}$ | B. | P损=$\frac{{U}^{2}S}{ρL}$ | C. | P损=$\frac{{P}^{2}ρL}{{U}^{2}S}$ | D. | P用=P-$\frac{{U}^{2}S}{ρL}$ | ||||
| E. | P用=P(1-$\frac{PρL}{{U}^{2}S}$) |
7. 如图所示,物体A、B放在物体C上,水平力F作用于A上,使A、B、C一起向左做匀速运动,则各接触面间的摩擦力的情况是( )
如图所示,物体A、B放在物体C上,水平力F作用于A上,使A、B、C一起向左做匀速运动,则各接触面间的摩擦力的情况是( )
 如图所示,物体A、B放在物体C上,水平力F作用于A上,使A、B、C一起向左做匀速运动,则各接触面间的摩擦力的情况是( )
如图所示,物体A、B放在物体C上,水平力F作用于A上,使A、B、C一起向左做匀速运动,则各接触面间的摩擦力的情况是( )| A. | A对C有向左的摩擦力 | B. | C对B有向左的摩擦力 | ||
| C. | 物体C受到一个摩擦力的作用 | D. | 物体C受到三个摩擦力的作用 |
8. 如图所示,两个$\frac{3}{4}$竖直圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA和hB,下列说法正确的是( )
如图所示,两个$\frac{3}{4}$竖直圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA和hB,下列说法正确的是( )
 如图所示,两个$\frac{3}{4}$竖直圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA和hB,下列说法正确的是( )
如图所示,两个$\frac{3}{4}$竖直圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA和hB,下列说法正确的是( )| A. | 若使小球A沿轨道运动并且从最高点飞出,释放的最小高度为$\frac{5R}{2}$ | |
| B. | 若使小球B沿轨道运动并且从最高点飞出,释放的最小高度为$\frac{3R}{2}$ | |
| C. | 适当调整hA,可使A球从轨道最高点飞出后,恰好落在轨道右端口处 | |
| D. | 适当调整hB,可使B球从轨道最高点飞出后,恰好落在轨道右端口处 |
 如图所示,物体在受到一水平向左的拉力F=6N作用下,以v=4m/s的初速度沿水平面向右运动,已知物体与水平面的动摩擦因数μ=0.2,物体质量m=2kg,g取10m/s2,z则物体所受摩擦力大小为4N,方向为水平向左,物体向右运动的最大位移为1.6m.
如图所示,物体在受到一水平向左的拉力F=6N作用下,以v=4m/s的初速度沿水平面向右运动,已知物体与水平面的动摩擦因数μ=0.2,物体质量m=2kg,g取10m/s2,z则物体所受摩擦力大小为4N,方向为水平向左,物体向右运动的最大位移为1.6m.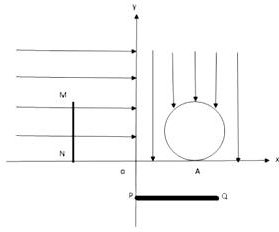 如图所示,在直角坐标系XOY的第二象限内,存在水平向右的匀强电场,电场强度大小为E0,M(-L,L)H和N(一L,0)两点的连线上有一个产生粒子的发生器装置,产生质量均为m,电荷量均为q的初速度为零的带正电的粒子,不计粒子的重力和粒子之间的相互作用,且整个装置处于真空中;在第一象限中,存在着竖直向下的匀强电场,电场强度大小为E0,圆形空间内没有电场,圆的直径为L,与X轴相切A点,A点的坐标为(L,0),在第四象限内距离x轴$\frac{\sqrt{3}}{3}$L的位置有一个平行于X轴拉为$\frac{4}{3}$L的荧光屏PQ,
如图所示,在直角坐标系XOY的第二象限内,存在水平向右的匀强电场,电场强度大小为E0,M(-L,L)H和N(一L,0)两点的连线上有一个产生粒子的发生器装置,产生质量均为m,电荷量均为q的初速度为零的带正电的粒子,不计粒子的重力和粒子之间的相互作用,且整个装置处于真空中;在第一象限中,存在着竖直向下的匀强电场,电场强度大小为E0,圆形空间内没有电场,圆的直径为L,与X轴相切A点,A点的坐标为(L,0),在第四象限内距离x轴$\frac{\sqrt{3}}{3}$L的位置有一个平行于X轴拉为$\frac{4}{3}$L的荧光屏PQ,