题目内容
8. 如图所示,两个$\frac{3}{4}$竖直圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA和hB,下列说法正确的是( )
如图所示,两个$\frac{3}{4}$竖直圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA和hB,下列说法正确的是( )| A. | 若使小球A沿轨道运动并且从最高点飞出,释放的最小高度为$\frac{5R}{2}$ | |
| B. | 若使小球B沿轨道运动并且从最高点飞出,释放的最小高度为$\frac{3R}{2}$ | |
| C. | 适当调整hA,可使A球从轨道最高点飞出后,恰好落在轨道右端口处 | |
| D. | 适当调整hB,可使B球从轨道最高点飞出后,恰好落在轨道右端口处 |
分析 小球A恰好能到A轨道的最高点时,轨道对小球无作用力,由重力提供小球的向心力,由牛顿第二定律即可求得小球到达轨道最高点的最小速度.
小球恰好能到B轨道的最高点时,速度为零,根据机械能守恒求出hA和hB.根据最高点的临界速度求出小球最高点飞出的水平位移的最小值.
解答 解:A、若小球A恰好能到A轨道的最高点时,由重力提供小球的向心力,由牛顿第二定律得:
mg=m$\frac{{v}_{A}^{2}}{R}$,vA=$\sqrt{gR}$.
根据机械能守恒定律得,mg(hA-2R)=$\frac{1}{2}$mv2,解得:hA=$\frac{5}{2}$R;故A正确,B错误;
C、小球A从最高点飞出后做平抛运动,下落R高度时,水平位移的最小值为 xA=vA$\sqrt{\frac{2R}{g}}$=$\sqrt{gR}$•$\frac{2R}{g}$=$\sqrt{2}$R>R,所以小球A从轨道最高点飞出后一定落在轨道右端口外侧.故C错误.
D、小球恰好能到B轨道的最高点时,临界速度为零,适当调整hB,B可以落在轨道右端口处.故D正确.
故选:AD
点评 本题是向心力、机械能守恒定律、平抛运动的综合,关键要抓住A轨道与轻绳系的球模型相似,B轨道与轻杆固定的球模型相似,要注意临界条件的不同.

练习册系列答案
相关题目
19. 如图所示,空间有一固定点电荷Q,电性未知.虚线为其电场的三个等势面.相邻等势面电势差相等.曲线ABC为带电粒子m的轨迹;曲线DEF为带电粒子n的轨迹.其中A、C、D、F为轨迹与最外一个等势面的交点.B、E为轨迹与中间一个等势面的交点,B、E为轨迹与中间一个等势面的交点.若m在A点、n在D点二者有相等的动能,不计重力和m、n间的相互作用,下列说法正确的是( )
如图所示,空间有一固定点电荷Q,电性未知.虚线为其电场的三个等势面.相邻等势面电势差相等.曲线ABC为带电粒子m的轨迹;曲线DEF为带电粒子n的轨迹.其中A、C、D、F为轨迹与最外一个等势面的交点.B、E为轨迹与中间一个等势面的交点,B、E为轨迹与中间一个等势面的交点.若m在A点、n在D点二者有相等的动能,不计重力和m、n间的相互作用,下列说法正确的是( )
 如图所示,空间有一固定点电荷Q,电性未知.虚线为其电场的三个等势面.相邻等势面电势差相等.曲线ABC为带电粒子m的轨迹;曲线DEF为带电粒子n的轨迹.其中A、C、D、F为轨迹与最外一个等势面的交点.B、E为轨迹与中间一个等势面的交点,B、E为轨迹与中间一个等势面的交点.若m在A点、n在D点二者有相等的动能,不计重力和m、n间的相互作用,下列说法正确的是( )
如图所示,空间有一固定点电荷Q,电性未知.虚线为其电场的三个等势面.相邻等势面电势差相等.曲线ABC为带电粒子m的轨迹;曲线DEF为带电粒子n的轨迹.其中A、C、D、F为轨迹与最外一个等势面的交点.B、E为轨迹与中间一个等势面的交点,B、E为轨迹与中间一个等势面的交点.若m在A点、n在D点二者有相等的动能,不计重力和m、n间的相互作用,下列说法正确的是( )| A. | m、n可能带同种电荷 | |
| B. | m在B点、n在E点二者的动能不相等 | |
| C. | m从A经B到C的过程中动能先减小后增大 | |
| D. | 内、中两个等势面的半径之差应小于中、外两个等势面的半径之差 |
16. 如图所示,E为电池,L是直流电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个完全相同的灯泡,S是控制电路的开关.对于这个电路,下列说法正确的是( )
如图所示,E为电池,L是直流电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个完全相同的灯泡,S是控制电路的开关.对于这个电路,下列说法正确的是( )
 如图所示,E为电池,L是直流电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个完全相同的灯泡,S是控制电路的开关.对于这个电路,下列说法正确的是( )
如图所示,E为电池,L是直流电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个完全相同的灯泡,S是控制电路的开关.对于这个电路,下列说法正确的是( )| A. | 刚闭合S的瞬间,灯泡D1、D2的亮度相同 | |
| B. | 刚闭合S的瞬间,灯泡D2比灯泡D1亮 | |
| C. | 闭合S,待电路达到稳定后,D1熄灭,D2比S刚闭合时更亮 | |
| D. | 闭合S,待电路达到稳定后,再将S断开,D2立即熄灭,D1闪亮后熄灭 |
3.关于矢量和标量,下列说法中正确的是( )
| A. | 矢量是既有大小又有方向的物理量 | B. | 标量是既有大小又有方向的物理量 | ||
| C. | 位移-10 m比5 m小 | D. | -10N比5N小 |
17. 如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,质量为m、电阻为R的正方形线圈abcd边长为L(L<d),将线圈在磁场上方高h处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场是速度也为v0,则线圈穿越磁场的过程中(从cd边刚入磁场一直到ab边刚离开磁场)( )
如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,质量为m、电阻为R的正方形线圈abcd边长为L(L<d),将线圈在磁场上方高h处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场是速度也为v0,则线圈穿越磁场的过程中(从cd边刚入磁场一直到ab边刚离开磁场)( )
 如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,质量为m、电阻为R的正方形线圈abcd边长为L(L<d),将线圈在磁场上方高h处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场是速度也为v0,则线圈穿越磁场的过程中(从cd边刚入磁场一直到ab边刚离开磁场)( )
如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,质量为m、电阻为R的正方形线圈abcd边长为L(L<d),将线圈在磁场上方高h处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场是速度也为v0,则线圈穿越磁场的过程中(从cd边刚入磁场一直到ab边刚离开磁场)( )| A. | 线圈产生的焦耳热为2mgd | B. | 线圈产生的焦耳热为2mgL | ||
| C. | 线圈的最小速度可能为$\frac{mgR}{{B}^{2}{L}^{2}}$ | D. | 线圈的最小速度一定为$\sqrt{2g(h+L-d)}$ |
18. 如图所示,质量为m的人,用绳子通过滑轮拉质量为M的物体.不计绳的质量和滑轮摩擦力,当人拉绳子向右走一步,系统仍保持平衡,下面说法正确的是( )
如图所示,质量为m的人,用绳子通过滑轮拉质量为M的物体.不计绳的质量和滑轮摩擦力,当人拉绳子向右走一步,系统仍保持平衡,下面说法正确的是( )
 如图所示,质量为m的人,用绳子通过滑轮拉质量为M的物体.不计绳的质量和滑轮摩擦力,当人拉绳子向右走一步,系统仍保持平衡,下面说法正确的是( )
如图所示,质量为m的人,用绳子通过滑轮拉质量为M的物体.不计绳的质量和滑轮摩擦力,当人拉绳子向右走一步,系统仍保持平衡,下面说法正确的是( )| A. | 人对地面的压力减少 | B. | 地面给人的摩擦力增加 | ||
| C. | 人对地面的作用力减少 | D. | 绳子的拉力变大 |
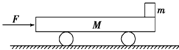 如图所示,质量M=2kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=6N,当小车向右运动的速度达到3m/s时,在小车前端轻轻地放上一个大小不计,质量为m=1kg的小物块,物块与小车间的动摩擦因数μ=0.4,小车足够长(取g=10m/s2).求:
如图所示,质量M=2kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=6N,当小车向右运动的速度达到3m/s时,在小车前端轻轻地放上一个大小不计,质量为m=1kg的小物块,物块与小车间的动摩擦因数μ=0.4,小车足够长(取g=10m/s2).求: 如图所示,一质量为M的木板静止在光滑的水平面上,在其右端放一质量m为的木块,一质量为m0的子弹以速度v0迅速击中木板并停在木板中,则此时木板获得的速度v=$\frac{{m}_{0}{v}_{0}}{M+{m}_{0}}$.
如图所示,一质量为M的木板静止在光滑的水平面上,在其右端放一质量m为的木块,一质量为m0的子弹以速度v0迅速击中木板并停在木板中,则此时木板获得的速度v=$\frac{{m}_{0}{v}_{0}}{M+{m}_{0}}$.