题目内容
20.在粗糙的水平桌面上有两个静止的木块A和B,A的质量为B的2倍,两者相距为d,已知两木块与桌面之间的动摩擦因数均为μ,现给A一初速度$\sqrt{\frac{13μgd}{5}}$,使A与B发生弹性正碰,碰撞时间极短,重力加速度大小为g.求两木块都停止运动时的距离.分析 A向B运动的过程中摩擦力做功,由动能定理即可求出A与B碰撞前的速度;碰撞过程中A、B组成的系统动量守恒,结合动量守恒定律和机械能守恒,表示出碰撞后的A、B的速度,最后结合位移关系即可求解.
解答 解:设A的初速度大小为v0,A与B碰撞前的速度为v,由动能定理得:-μ2mgd=$\frac{1}{2}$2mv2-$\frac{1}{2}$2mv02
在发生碰撞前的瞬间,选择A的运动方向为正方向,在碰撞后的瞬间,A和B的速度分别为v1和v2.
在碰撞过程中,由能量守恒定律和动量守恒定律.得
$\frac{1}{2}$2mv2=$\frac{1}{2}$2mv12+$\frac{1}{2}$mv22,
2mv=2mv1+mv2
设碰撞后A和B运动的距离分别为d1和d2,
由动能定理得-μ•2mgd1=0-$\frac{1}{2}$•2mv12.
-μmgd2=0-$\frac{1}{2}$mv22.
按题意有:x=d2-d1.
联立解得:x=$\frac{1}{2}d$
答:两木块都停止运动时的距离是$\frac{1}{2}d$.
点评 本题综合考查了动量守恒定律、动能定理、能量守恒定律,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
10. 目前,世界上正在研究一种新型发电机叫磁流体发电机,如图表示它的原理:将一束等离子体喷射入磁场,在磁场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压,以下说法正确的是( )
目前,世界上正在研究一种新型发电机叫磁流体发电机,如图表示它的原理:将一束等离子体喷射入磁场,在磁场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压,以下说法正确的是( )
 目前,世界上正在研究一种新型发电机叫磁流体发电机,如图表示它的原理:将一束等离子体喷射入磁场,在磁场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压,以下说法正确的是( )
目前,世界上正在研究一种新型发电机叫磁流体发电机,如图表示它的原理:将一束等离子体喷射入磁场,在磁场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压,以下说法正确的是( )| A. | 其他条件不变,只减小磁感应强度,UAB增大 | |
| B. | 其他条件不变,只减小两板之间的距离,UAB增大 | |
| C. | 其他条件不变,只减小射入速度,UAB增大 | |
| D. | 流过电阻R的电流方向从B板经过R到A板 |
11.关于力学单位制,下列说法中正确的是( )
| A. | kg、m、N是基本单位 | |
| B. | 在国际单位制中,牛顿第二定律的表达式才是F=ma | |
| C. | kg、N、m/s都是导出单位 | |
| D. | 在国际单位制中,质量的基本单位是kg,也可以是g |
8.关于紫外线,下列说法不正确的是( )
| A. | 紫外线有灭菌消毒作用 | |
| B. | 紫外线能使荧光物质发光 适当的紫外线照射,有助于人体合成维生素 | |
| C. | 对骨骼的生长和身体的健康等许多方面都有好处 | |
| D. | 紫外线对人类总是有益的 |
6.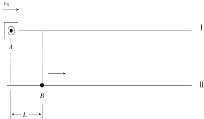 小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )
小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )
 小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )
小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )| A. | 欲使彩弹击中耙心,可在t=5.0s时发出彩弹 | |
| B. | 若彩弹在最短时间内击中靶心,则击中靶心时彩弹的速度是50m/s | |
| C. | 若要求在t=10.0s时发出彩弹并击中靶心,则彩弹枪与Ⅱ号水平直线的夹角(锐角)是53° | |
| D. | 若要求在t=10.0s时发出彩弹并击中靶心,则彩弹飞行的时间是0.5s |

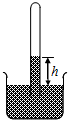 如图,开口向下的玻璃管插入水银槽中,管内封闭了一段气体,气体压强为p,管内外水银面高度差为h.若增大外界大气压强,则h将增大(增大、减小、不变);p将增大(增大、减小、不变)
如图,开口向下的玻璃管插入水银槽中,管内封闭了一段气体,气体压强为p,管内外水银面高度差为h.若增大外界大气压强,则h将增大(增大、减小、不变);p将增大(增大、减小、不变) 如图所示,光滑的平行导轨倾角为θ=45°,处在竖直向下的匀强磁场中,磁感应强度B=1T,导轨中接入电动势为E=1.5 V、内阻为r=0.2Ω的直流电源,电路中电动机的电阻为R=0.3Ω,其余电阻不计.将质量为m=0.1 kg、长度为L=1 m的导体棒放在平行导轨上恰好能够处于静止状态,g取10m/s2.求:
如图所示,光滑的平行导轨倾角为θ=45°,处在竖直向下的匀强磁场中,磁感应强度B=1T,导轨中接入电动势为E=1.5 V、内阻为r=0.2Ω的直流电源,电路中电动机的电阻为R=0.3Ω,其余电阻不计.将质量为m=0.1 kg、长度为L=1 m的导体棒放在平行导轨上恰好能够处于静止状态,g取10m/s2.求: