题目内容

18．如图所示，a、b、c、d是位于同竖直平面内圆周上四点，a为圆周的最高点，b为最低点．ac、bd为两根固定的光滑细杆，每根杆上各套着一个小滑环，两个滑环都从杆的最高点无初速释放，证明：两个滑环的滑行时间相等．

分析 先对任一滑环受力分析后，根据牛顿第二定律计算出滑环沿任意一根杆滑动的加速度，然后根据位移时间关系公式计算出时间，对表达式分析，得出结论．

解答 解：设任一杆与竖直方向夹角为β．
沿杆下滑加速度　　a=g•cosβ
下滑位移　　x=2R•cosβ
下滑时间 $t=\sqrt{\frac{2x}{a}}=\sqrt{\frac{g}{R}}$
可知，t与下滑的角度无关，故两条不同路径运动时间相等．
证明：见上．

点评 本题关键从众多的杆中抽象出一根杆，假设其与竖直方向夹角为β，然后根据牛顿第二定律求出加速度，再根据运动学公式求出时间表达式来证明结论．

练习册系列答案
相关题目
8．如图所示，一个理想变压器原线圈和副线圈的匝数分别为n1和n2，正常工作时输入和输出的电压分别为U1和U2，已知n1＞n2，则（　　）
A．该变压器为降压变压器，U1＞U2B．该变压器为降压变压器，U2＞U1
C．该变压器为升压变压器，U1＞U2D．该变压器为升压变压器，U2＞U1
9．在空中下落的物体，由于空气阻力随着速度的增大而增大，最终会达到一个恒定的速度，称之为收尾速度．一物体质量为m，将它从空中静止释放，最后物体的收尾速度为v，重力加速度为g，下列说法正确的是（　　）
A．若测得物体从释放至达到收尾速度所用时间为t，则物体下落的位移为$\frac{vt}{2}$
B．若测得某一时刻物体下落时的加速度为a，则物体此时的速度为$\sqrt{2ah}$
C．若测得某时物体的加速度为a，此时物体受到的空气阻力为mg-ma
D．若测得物体下落t时间，通过的位移为y，则该过程的平均速度一定为$\frac{y}{t}$
6．如图所示，质量为m的球置于斜面上，被一个竖直挡板挡住．现用一个恒力F拉斜面，使斜面在水平面上向右做加速度为a的匀加速直线运动，忽略一切摩擦，以下说法中正确的是（　　）
A．若加速度足够小，竖直挡板对球的弹力可能为零
B．若加速度足够大，斜面对球的弹力可能为零
C．斜面对球的弹力大小与加速度大小无关
D．挡板对球的弹力大小与加速度大小无关
13．一足够长水平浅色传送带以v0=4m/s匀速运动，现将一可视为质点的小煤块轻放在其上方，已知煤块与传送带间的动摩擦因数为μ=0.2．经过一定时间后达到共同速度．令传送带突然停下，以后不再运动，到最后煤块也停下．已知重力加速度为g=10m/s2．则（　　）
A．煤块经过时间t=4s与皮带第一次共速
B．煤块在传送带上划出的轨迹长度为8米
C．煤块在传送带上划出的轨迹长度为4米
D．煤块经过时间t=2s距离出发点最远
3．如图，用两根绳子把质量为10千克的物体W吊在水平杆子AB上，∠ACW=150°，∠BCW=120°，如果绳子的质量忽略不计，求A处和B处所受力的大小．
10．A、B、C为三个相同的金属小球，A、B带等量的同种电荷，作用力为F，C不带电，让C先与A接触后再与B接触，然后移开，则A、B间的作用力是（　　）
A．斥力，$\frac{3F}{8}$B．斥力，$\frac{F}{8}$C．0D．引力，$\frac{F}{4}$
14．在水平匀强电场中，将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置，释放后，M、N保持静止，则（　　）
A．M的带电量比N的大B．M带正电荷、N带负电荷
C．移动过程中匀强电场对M做负功D．移动过程中匀强电场对N做正功
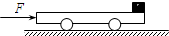15．光滑的水平面上静置一足够长、质量M=8kg的小车，如图所示．现在小车的左端施加一大小F=8N的水平推力，当小车向右运动的速度达到v0=1.5m/s时，在小车右端轻轻地放上一质量m=2kg的小物块（可视为质点）．已知小物块与小车间的动摩擦因数μ=0.2，取g=10m/s2．求：
（1）小物块放在小车上，两者达到相同的速度前，小物块和小车的加速度大小a1和a2；
（2）从小物块放在小车上，到两者刚达到相同的速度所需的时间t；
（3）从小物块放在小车上，到两者刚达到相同的速度的过程中，小物块通过的位移大小x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网