题目内容
4. 如图所示,一夹子夹住木块,在力 F 作用下向上提升.夹子和木块的质量分别为m、M,夹子与木块两侧面的最大静摩擦力均为f.若木块不滑动,力F的最大值是( )
如图所示,一夹子夹住木块,在力 F 作用下向上提升.夹子和木块的质量分别为m、M,夹子与木块两侧面的最大静摩擦力均为f.若木块不滑动,力F的最大值是( )| A. | $\frac{2f(m+M)}{M}$-(m+M)g | B. | $\frac{2f(m+M)}{m}$ | C. | $\frac{2f(m+M)}{M}$ | D. | $\frac{2f(m+M)}{m}$-(m+M)g |
分析 隔离对木块分析,通过牛顿第二定律求出木块的最大加速度,再对整体分析,运用牛顿第二定律求出拉力F的最大值.
解答 解:对木块分析得:2f-Mg=Ma,解得木块的最大加速度为:a=$\frac{2f}{M}-g$
对整体分析得:F-(M+m)g=(M+m)a
将a代入解得:F=$\frac{2f(m+M)}{M}$.故C正确,A、B、D错误.
故选:C.
点评 解决本题的关键能够正确地进行受力分析,运用牛顿第二定律进行求解.注意整体法和隔离法的运用.

练习册系列答案
相关题目
15. 如图所示,粗糙斜面与竖直方向保持一定夹角,三个相同物块a、b、c在斜面上的A、B、C三点,随斜面一起绕过最低点O的竖直轴以角速度ω0匀速转动,b恰好不受斜面摩擦力作用,且a、b、c均相对斜面保持静止,则以下判断正确的是( )
如图所示,粗糙斜面与竖直方向保持一定夹角,三个相同物块a、b、c在斜面上的A、B、C三点,随斜面一起绕过最低点O的竖直轴以角速度ω0匀速转动,b恰好不受斜面摩擦力作用,且a、b、c均相对斜面保持静止,则以下判断正确的是( )
 如图所示,粗糙斜面与竖直方向保持一定夹角,三个相同物块a、b、c在斜面上的A、B、C三点,随斜面一起绕过最低点O的竖直轴以角速度ω0匀速转动,b恰好不受斜面摩擦力作用,且a、b、c均相对斜面保持静止,则以下判断正确的是( )
如图所示,粗糙斜面与竖直方向保持一定夹角,三个相同物块a、b、c在斜面上的A、B、C三点,随斜面一起绕过最低点O的竖直轴以角速度ω0匀速转动,b恰好不受斜面摩擦力作用,且a、b、c均相对斜面保持静止,则以下判断正确的是( )| A. | a、b、c所受斜面的支持力大小相等 | |
| B. | a受沿斜面向上的摩擦力,c受沿斜面向下的摩擦力 | |
| C. | 若斜面匀速转动的角速度小于ω0,则a可能不受摩擦力作用 | |
| D. | 若斜面匀速转动的角速度小于ω0,则c可能不受摩擦力作用 |
19.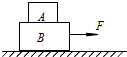 如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F则摩擦力f1和f2的大小( )
如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F则摩擦力f1和f2的大小( )
 如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F则摩擦力f1和f2的大小( )
如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F则摩擦力f1和f2的大小( )| A. | f1不变、f2变大 | B. | f1变大、f2不变 | C. | f1和f2都变大 | D. | f1和f2都不变 |
9. 如图所示,粗糙的水平地面上有一斜劈,斜劈上一物块在沿斜面向上的拉力 F作用下沿斜面以速度v0匀速上滑,斜劈保持静止,则地面对斜劈的摩擦力( )
如图所示,粗糙的水平地面上有一斜劈,斜劈上一物块在沿斜面向上的拉力 F作用下沿斜面以速度v0匀速上滑,斜劈保持静止,则地面对斜劈的摩擦力( )
 如图所示,粗糙的水平地面上有一斜劈,斜劈上一物块在沿斜面向上的拉力 F作用下沿斜面以速度v0匀速上滑,斜劈保持静止,则地面对斜劈的摩擦力( )
如图所示,粗糙的水平地面上有一斜劈,斜劈上一物块在沿斜面向上的拉力 F作用下沿斜面以速度v0匀速上滑,斜劈保持静止,则地面对斜劈的摩擦力( )| A. | 等于零 | |
| B. | 不为零,方向向右 | |
| C. | 不为零,方向向左 | |
| D. | 不为零,v0较大时方向向右,v0较小时向左 |
16. 如图甲所示,静止在水平地面上的物块A,受到水平拉力F的作用,F与时间t的关系如图乙所示,设物块与地面之间的最大静摩擦力fm大小与滑动摩擦力大小相等,则( )
如图甲所示,静止在水平地面上的物块A,受到水平拉力F的作用,F与时间t的关系如图乙所示,设物块与地面之间的最大静摩擦力fm大小与滑动摩擦力大小相等,则( )
 如图甲所示,静止在水平地面上的物块A,受到水平拉力F的作用,F与时间t的关系如图乙所示,设物块与地面之间的最大静摩擦力fm大小与滑动摩擦力大小相等,则( )
如图甲所示,静止在水平地面上的物块A,受到水平拉力F的作用,F与时间t的关系如图乙所示,设物块与地面之间的最大静摩擦力fm大小与滑动摩擦力大小相等,则( )| A. | 0~t0时间内力F的功率逐渐增大 | |
| B. | t1时刻A的运动方向开始相反 | |
| C. | t2时刻A的速度最大 | |
| D. | t2时刻A的加速度大小大于t0时刻A的加速度大小 |
 如图所示的等壁天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽度为L,共N匝,线圈下端悬在匀强磁场中,磁场方向垂直纸面.当线圈中未通有电流时,在天平左右两边加上质量各为m1、m2的砝码,天平平衡.当通以图示方向的电流I时,右边再加上质量为m的砝码后天平重新平衡,则线圈的质量为m1-m2,匀强磁场的磁感应强度大小为$\frac{mg}{2NIL}$.
如图所示的等壁天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽度为L,共N匝,线圈下端悬在匀强磁场中,磁场方向垂直纸面.当线圈中未通有电流时,在天平左右两边加上质量各为m1、m2的砝码,天平平衡.当通以图示方向的电流I时,右边再加上质量为m的砝码后天平重新平衡,则线圈的质量为m1-m2,匀强磁场的磁感应强度大小为$\frac{mg}{2NIL}$. 如图所示,在x轴上方有一匀强电场,场强大小为E,方向竖直向下,在x轴下方有一匀强磁场,磁感强度为B,方向垂直纸面向里.在x轴上有一点P,离原点距离为a,现有一带电量为正q,质量为m的粒子,从0<x<a区间某点由静止开始释放后,能经过P点,试讨论释放点坐标x、y应满足什么关系?(E、B均在x>0区域,粒子重力不计)
如图所示,在x轴上方有一匀强电场,场强大小为E,方向竖直向下,在x轴下方有一匀强磁场,磁感强度为B,方向垂直纸面向里.在x轴上有一点P,离原点距离为a,现有一带电量为正q,质量为m的粒子,从0<x<a区间某点由静止开始释放后,能经过P点,试讨论释放点坐标x、y应满足什么关系?(E、B均在x>0区域,粒子重力不计)