题目内容
19. 如图所示,半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁场方向垂直纸面向里,匀强磁场的磁感应强度为B,筒形场区的边界由弹性材料构成.一个质量为m、电荷量为q的正离子(不计重力)以某一速度从简壁上的小孔M进入筒中,速度方向与半径成θ=300夹角,并垂直于磁场方向.离子和筒壁的碰撞无能量和电荷量的损失.若选择合适的进入速度,离子可以从M孔射出.问:
如图所示,半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁场方向垂直纸面向里,匀强磁场的磁感应强度为B,筒形场区的边界由弹性材料构成.一个质量为m、电荷量为q的正离子(不计重力)以某一速度从简壁上的小孔M进入筒中,速度方向与半径成θ=300夹角,并垂直于磁场方向.离子和筒壁的碰撞无能量和电荷量的损失.若选择合适的进入速度,离子可以从M孔射出.问:(1)离子的速度多大时,离子可以在最短的时间内返回M孔?最短的时间是多少?
(2)如果离子与筒壁发生两次碰撞后从M孔射出,离子的速率是多大?从进入圆筒到返回M孔经历的时间是多少?
(3)如果离子与筒壁发生n次碰撞后从M孔射出,离子的速率又是多大?
分析 (1)离子与筒壁碰撞一次返回M孔时用的时间最短,作出粒=离子运动轨迹,求出粒子轨道半径,应用牛顿第二定律求出粒子的速度,根据离子转过的圆心角与周期公式求出粒子的运动时间.
(2)作出离子与筒壁碰撞两次的运动轨迹,求出离子轨道半径,应用牛顿第二定律求出粒子的速度,根据离子转过的圆心角与周期公式求出粒子的运动时间.
(3)作出离子的运动轨迹,求出离子轨道半径,应用牛顿第二定律求出粒子的速度,根据离子转过的圆心角与周期公式求出粒子的运动时间.
解答 解:(1)离子与筒壁碰撞一次返回M孔运动时间最短,其运动轨迹如图所示:
由几何知识可得:r=2R,
洛伦兹力提供向心力,由牛顿第二定律得:qv1B=m$\frac{{v}_{1}^{2}}{r}$,解得:v1=$\frac{2qBR}{m}$,
离子在磁场中每段圆弧对应的圆心角α=60°,
离子在磁场中的运动时间:t1=$\frac{2α}{360°}$T=$\frac{2×60°}{360°}$×$\frac{2πm}{qB}$=$\frac{2πm}{3qB}$;
(2)离子与筒壁发生两次碰撞后从M孔射出时运动轨迹如图所示: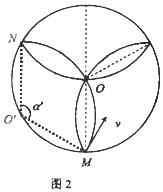
由几何知识得:r=R,离子做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qv2B=m$\frac{{v}_{2}^{2}}{r}$,解得:v2=$\frac{qBR}{m}$,
离子在磁场中走过的每段圆弧对应的圆心角:α′=120°,
离子的运动时间:t2=T=$\frac{2πm}{qB}$;
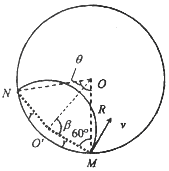
(3)设碰撞n次后返回M孔时,每相邻两次碰撞点对应的场区的圆心角为θ,
必须满足:(n+1)θ=2π,由几何知识得:$\frac{θ}{2}$+β=$\frac{2π}{3}$,$\frac{R}{sinβ}$=$\frac{r}{sin\frac{θ}{2}}$,解得:r=$\frac{2Rtan\frac{π}{n+1}}{\sqrt{3}+tan\frac{π}{n+1}}$,
由牛顿第二定律得:qvnB=m$\frac{{v}_{n}^{2}}{r}$,解得:vn=$\frac{2qBR}{m}$$\frac{tan\frac{π}{n+1}}{\sqrt{3}+tan\frac{π}{n+1}}$;
答:(1)离子的速度为$\frac{2qBR}{m}$时,离子可以在最短的时间内返回M孔,最短的时间是$\frac{2πm}{3qB}$;
(2)如果离子与筒壁发生两次碰撞后从M孔射出,离子的速率是$\frac{qBR}{m}$,从进入圆筒到返回M孔经历的时间是$\frac{2πm}{qB}$;
(3)如果离子与筒壁发生n次碰撞后从M孔射出,离子的速率是$\frac{2qBR}{m}$$\frac{tan\frac{π}{n+1}}{\sqrt{3}+tan\frac{π}{n+1}}$.
点评 本题考查了离子在磁场中的运动,分析清楚离子运动过程、作出离子运动轨迹、应用几何知识求出离子轨道半径与圆心角是解题的关键,应用牛顿第二定律可以求出粒子的速度.

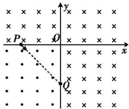 如图所示,在xOy平面内存在磁感应强度大小为B的匀强磁场,第一、二、四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外.P(-L,0)、Q(0,-L)为坐标轴上的两个点.现有一电子从P点沿PQ方向射出,不计电子的重力,下列说法正确的是( )
如图所示,在xOy平面内存在磁感应强度大小为B的匀强磁场,第一、二、四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外.P(-L,0)、Q(0,-L)为坐标轴上的两个点.现有一电子从P点沿PQ方向射出,不计电子的重力,下列说法正确的是( )| A. | 若电子从P点出发恰好经原点O第一次射出磁场分界线,则电子运动的路程一定为$\frac{πL}{2}$ | |
| B. | 若电子从P点出发经原点O到达Q点,则电子运动的路程一定为πL | |
| C. | 若电子从P点出发经原点O到达Q点,则电子运动的路程一定为2πL | |
| D. | 若电子从P点出发经原点O到达Q点,则电子运动的路程可能为πL,也可能为2πL |
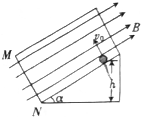 绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )
绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )| A. | 匀强磁场磁感应强度的取值范围为0≤B≤$\frac{mg}{q{v}_{0}}$ | |
| B. | 匀强磁场磁感应强度的取值范围为0≤B≤$\frac{mgcosα}{q{v}_{0}}$ | |
| C. | 小球在斜面做变加速曲线运动 | |
| D. | 小球到达底边MN的时间t=$\sqrt{\frac{2h}{gsi{n}^{2}α}}$ |
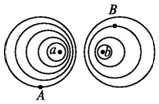 空间两点放置两个异种点电荷a、b,其所带电荷量分别为qa和qb,其产生的电场的等势面如图所示,且相邻等势面间的电势差均相等,电场中A、B两点间的电势大小的关系为φA>φB,由此可以判断出a为正电荷,且有qa<qb.错(判断对错)
空间两点放置两个异种点电荷a、b,其所带电荷量分别为qa和qb,其产生的电场的等势面如图所示,且相邻等势面间的电势差均相等,电场中A、B两点间的电势大小的关系为φA>φB,由此可以判断出a为正电荷,且有qa<qb.错(判断对错)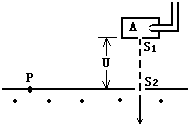 如图所示为测量某种离子的比荷的装置,让中性气体分子进入电离室A,在那里被电离成离子.这些离子从电离室的小孔飘出,从缝S1进入加速电场被加速,然后让离子从缝S2垂直进入匀强磁场,最后打在底片上的P点.已知加速电压为U,磁场的磁感应强度为B,缝S2与P之间的距离为a,离子从缝S1进入电场时的速度不计,求:
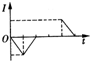
如图所示为测量某种离子的比荷的装置,让中性气体分子进入电离室A,在那里被电离成离子.这些离子从电离室的小孔飘出,从缝S1进入加速电场被加速,然后让离子从缝S2垂直进入匀强磁场,最后打在底片上的P点.已知加速电压为U,磁场的磁感应强度为B,缝S2与P之间的距离为a,离子从缝S1进入电场时的速度不计,求: 如图所示,边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场,一个直角边长为l的等腰直角三角形导线框所在平面与磁场方向垂直,导线框斜边的中线和虚线框的一条对角线恰好共线.从t=0开始,使导线框从图示位置开始以恒定速度沿对角线方向进入磁场,直到整个导线框离开磁场区域.用I表示导线框中的感应电流(逆时针方向为正),则下列表示I-t关系的图象中,正确的是( )
如图所示,边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场,一个直角边长为l的等腰直角三角形导线框所在平面与磁场方向垂直,导线框斜边的中线和虚线框的一条对角线恰好共线.从t=0开始,使导线框从图示位置开始以恒定速度沿对角线方向进入磁场,直到整个导线框离开磁场区域.用I表示导线框中的感应电流(逆时针方向为正),则下列表示I-t关系的图象中,正确的是( )


 固定在匀强磁场中的正方形导线框abcd,各边长为L,其中ab是一段电阻为R的均匀电阻丝,其余三边均为电阻可以忽略的铜线,磁感应强度为B的匀强磁场方向垂直纸面向里.现有一段与ab材料、粗细、长度均相同的电阻丝PQ架在导线框上,如图所示.若PQ以恒定速度v从ad滑向bc,当其滑过$\frac{L}{3}$的距离时,通过Pb段的电流多大?方向如何?
固定在匀强磁场中的正方形导线框abcd,各边长为L,其中ab是一段电阻为R的均匀电阻丝,其余三边均为电阻可以忽略的铜线,磁感应强度为B的匀强磁场方向垂直纸面向里.现有一段与ab材料、粗细、长度均相同的电阻丝PQ架在导线框上,如图所示.若PQ以恒定速度v从ad滑向bc,当其滑过$\frac{L}{3}$的距离时,通过Pb段的电流多大?方向如何? 如图所示,在直角坐标系的第Ⅱ象限中,一边长为L的正方形区域内存在磁感应强度大小为B、方向垂直xOy平面向里的匀强磁场,磁场的下边界与x轴重合,右边界与y轴重合,在第Ⅰ、Ⅳ象限x<L区域内存在沿y轴负方向的匀强电场,电场强度大小为E,在x>L区域内存在磁感应强度大小为B′、方向垂直纸面向里的矩形匀强磁场;一质量为m、电荷量为q的带正电的粒子(重力不计)以沿y轴负方向的速度进入第Ⅱ象限的匀强磁场区域,并从坐标原点O处沿x轴正方向射入匀强电场区域;
如图所示,在直角坐标系的第Ⅱ象限中,一边长为L的正方形区域内存在磁感应强度大小为B、方向垂直xOy平面向里的匀强磁场,磁场的下边界与x轴重合,右边界与y轴重合,在第Ⅰ、Ⅳ象限x<L区域内存在沿y轴负方向的匀强电场,电场强度大小为E,在x>L区域内存在磁感应强度大小为B′、方向垂直纸面向里的矩形匀强磁场;一质量为m、电荷量为q的带正电的粒子(重力不计)以沿y轴负方向的速度进入第Ⅱ象限的匀强磁场区域,并从坐标原点O处沿x轴正方向射入匀强电场区域;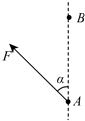 为使带负电的点电荷q在一匀强电场中沿直线匀速地由A运动到B,必须对该电荷施加一个恒力F,如图所示;若已知AB=0.5m,恒力F与AB的夹角α=37°,q=-3×10-7C,F=1.5×10-4N,A点电势φA=60V(不计重力,sin 37°=0.6 cos37°=0.8),求出电场强度的大小和B点的电势.
为使带负电的点电荷q在一匀强电场中沿直线匀速地由A运动到B,必须对该电荷施加一个恒力F,如图所示;若已知AB=0.5m,恒力F与AB的夹角α=37°,q=-3×10-7C,F=1.5×10-4N,A点电势φA=60V(不计重力,sin 37°=0.6 cos37°=0.8),求出电场强度的大小和B点的电势.