题目内容
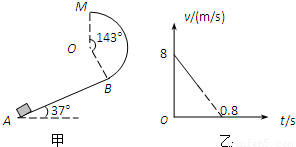
如图甲所示,一半径R=1m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示,若物块恰能到达M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:(1)物块经过M点的速度大小;
(2)物块经过B点的速度大小;
(3)物块与斜面间的动摩擦因数.
【答案】分析:(1)物块恰能到达M点,由重力提供向心力,由牛顿第二定律可求出物块经过M点的速度大小;
(2)物块从B点运动到M点的过程中,只有重力做功,由动能定理列式求出物块经过B点的速度大小;
(3)由速度图象的斜率求出加速度大小,判断出加速度方向,根据牛顿第二定律求解物块与斜面间的动摩擦因数.
解答:解:(1)据题,物块恰好能到达M点,则有
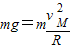
解得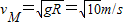
(2)物块从B点运动到M点的过程中,由动能定理得:
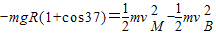
解得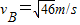
(3)由乙图可知,物体在斜面上运动时,加速度大小为a=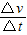 =
=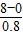 m/s2=10m/s2,方向沿斜面向下,由牛顿第二定律得:
m/s2=10m/s2,方向沿斜面向下,由牛顿第二定律得:
mgsin37°+μmgcos37°=ma
则 μ=0.5
答:
(1)物块经过M点的速度大小为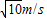 .
.
(2)物块经过B点的速度大小为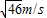 .
.
(3)物块与斜面间的动摩擦因数为0.5.
点评:本题是动能定理与圆周运动、速度图象、牛顿第二定律等知识的综合应用,把握解题规律是关键.
(2)物块从B点运动到M点的过程中,只有重力做功,由动能定理列式求出物块经过B点的速度大小;
(3)由速度图象的斜率求出加速度大小,判断出加速度方向,根据牛顿第二定律求解物块与斜面间的动摩擦因数.
解答:解:(1)据题,物块恰好能到达M点,则有
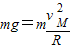
解得
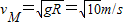
(2)物块从B点运动到M点的过程中,由动能定理得:
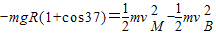
解得
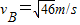
(3)由乙图可知,物体在斜面上运动时,加速度大小为a=
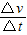 =
=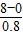 m/s2=10m/s2,方向沿斜面向下,由牛顿第二定律得:
m/s2=10m/s2,方向沿斜面向下,由牛顿第二定律得:mgsin37°+μmgcos37°=ma
则 μ=0.5
答:
(1)物块经过M点的速度大小为
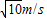 .
.(2)物块经过B点的速度大小为
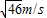 .
.(3)物块与斜面间的动摩擦因数为0.5.
点评:本题是动能定理与圆周运动、速度图象、牛顿第二定律等知识的综合应用,把握解题规律是关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图甲所示,一半径R=1.4m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示.若物块恰能达到M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:
如图甲所示,一半径R=1.4m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示.若物块恰能达到M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求: 如图甲所示,一半径R=1m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示,若物块恰能到达M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:
如图甲所示,一半径R=1m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示,若物块恰能到达M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:
 ;
; ;
; 。
。
