题目内容
19.如图1所示,在xOy坐标系中,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,紧靠极板的右边缘的有界匀强磁场区域由△ABO和举 行OBCD构成,其中∠0AB=60°,0D=OA.磁场方向垂直于x0y平面向里,D、A位于y轴上.位于极板左侧的粒子源沿x轴向右接连发射质量为m,、电荷量为+q、速度相同的带电粒子,现在0~3t0时间内两板间加上如图2所示的电压,已知t=0时刻进入两板间的粒子,在t0时刻射入磁场时,恰好不会从磁场边界射出磁场区域且圆心在x轴上,上述l、m、q、t0为已知量,U0=$\frac{m{l}^{2}}{q{{t}_{0}}^{2}}$,不考虑P、Q两板电压的变化对磁场的影响,也不考虑粒子的重力及粒子间的相互影响,求:
行OBCD构成,其中∠0AB=60°,0D=OA.磁场方向垂直于x0y平面向里,D、A位于y轴上.位于极板左侧的粒子源沿x轴向右接连发射质量为m,、电荷量为+q、速度相同的带电粒子,现在0~3t0时间内两板间加上如图2所示的电压,已知t=0时刻进入两板间的粒子,在t0时刻射入磁场时,恰好不会从磁场边界射出磁场区域且圆心在x轴上,上述l、m、q、t0为已知量,U0=$\frac{m{l}^{2}}{q{{t}_{0}}^{2}}$,不考虑P、Q两板电压的变化对磁场的影响,也不考虑粒子的重力及粒子间的相互影响,求:(1)t=0时刻进入两板间的带电粒子射入磁场时的速度;
(2)匀强磁场的磁感应强度的大小及磁场区域的面积;
(3)t=t0时刻进入两板间的带电粒子在匀强磁场中运动的时间.
分析 (1)根据题意可知粒子在两平行板间做类平抛运动,由平抛运动性质可分别求出粒子水平方向和竖直方向的速度,最后对这两个速度进行合成,由于速度为矢量需注意方向问题;
(2)需画出粒子运动轨迹,根据几何知识求出粒子运动半径,再求出磁感应强度的大小.由几何知识可求出AB边长,最后求出磁场区域面积;
(3)先判断粒子在磁场中运动轨迹,根据圆周运动公式求出粒子的运动时间.
解答 解:(1)t=0时刻进入电场的粒子t0时刻刚好射出电场,
带电粒子沿x轴分速度大小为${v}_{0}=\frac{l}{{t}_{0}}$
y轴负方向偏移距离$y=\frac{1}{2}\frac{{U}_{0}q}{ml}{{t}_{0}}^{2}=\frac{1}{2}l$
设粒子离开电场沿y轴负方向的分速度为,则有$\frac{1}{2}l=\frac{{v}_{y}}{2}{t}_{0}$
可知${v}_{y}=\frac{l}{{t}_{0}}$
射入磁场的速度${v}_{1}=\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\frac{\sqrt{2}l}{{t}_{0}}$,与y轴负方向夹角45°;
(2)设粒子在磁场中做匀变速圆周运动的半径为R1,
由几何关系得${R}_{1}=\frac{\sqrt{2}}{2}l$
$q{v}_{1}B=m\frac{{{v}_{1}}^{2}}{{R}_{1}}$
得$B=\frac{2m}{q{t}_{0}}$
设AB长为a,则由几何关系得$2{R}_{1}+\frac{l}{2}=a•sin60°$
得$a=\frac{2\sqrt{6}+\sqrt{3}}{3}l$
磁场区域的面积为:$S=\frac{1}{2}{a}^{2}cos30°+\frac{1}{4}{a}^{2}cos30°=(\frac{9\sqrt{3}}{8}+\frac{\sqrt{6}}{2})$l2.
(3)t0时刻进入两板间的带电粒子在两板间做匀速直线运动.
在2t0时刻沿x轴方向进入磁场,进入磁场后做圆周运动,
设半径为R2.
$q{v}_{0}B=m\frac{{{v}_{0}}^{2}}{{R}_{2}}$
得${R}_{2}=\frac{1}{2}l$
由于$\frac{a}{2}>{R}_{2}$,所以粒子不会从DC和BC边射出磁场.
粒子在磁场中运动的时间$t=\frac{π{R}_{2}}{{v}_{0}}=\frac{π{t}_{0}}{2}$
答:(1)t=0时刻进入两板间的带电粒子射入磁场时的速度为$\frac{\sqrt{2}l}{2}$,与y轴负方向夹角45°;
(2)匀强磁场的磁感应强度的大小为$\frac{2m}{q{t}_{0}}$及磁场区域的面积为$(\frac{9\sqrt{3}}{8}+\frac{\sqrt{6}}{2}){l}^{2}$;
(3)t=t0时刻进入两板间的带电粒子在匀强磁场中运动的时间为$\frac{π{t}_{0}}{2}$.
点评 本题属于带电粒子在组合场中的运动,主要考查考生综合分析问题能力,求解的关键是找到粒子的运动轨迹刚好和AB边相切,找到几何关系求出AB边的长度.第三问要通过计算判断再求解.

 如图所示,三个小球a、b、c分别从三个光滑斜面顶端由静止下滑,其中a、b所在的两光滑斜面的总长度相等,高度也相同,a、c所在斜面底边相同,若球经过图上斜面转折点时无能量损失,则下列说法正确的是( )
如图所示,三个小球a、b、c分别从三个光滑斜面顶端由静止下滑,其中a、b所在的两光滑斜面的总长度相等,高度也相同,a、c所在斜面底边相同,若球经过图上斜面转折点时无能量损失,则下列说法正确的是( )| A. | a比b后着地 | B. | a与c可能同时着地 | ||
| C. | a和b可能同时着地 | D. | a、b、c着地时速度大小可能相等 |
| A. | 肥皂泡呈彩色条纹是光的干涉现象造成的 | |
| B. | 从地面上观察,飞船上的时间进程比地面快 | |
| C. | 光的偏振现象说明光是一种横波 | |
| D. | 用光导纤维来传输图象和信息,这是利用了光的全反射原理 | |
| E. | X射线比γ射线的穿透能力更强 |
| A. | 2×1030kg | B. | 2×1031kg | C. | 2×1028kg | D. | 2×1032kg |

| A. | 这个电场可能是负的点电荷的电场 | |
| B. | 点电荷q在A点处受到的静电力比在B点处受到的静电力大 | |
| C. | 点电荷q在A点处的加速度比在B点处的加速度小 | |
| D. | 正点电荷q在B点释放后将沿着电场线运动 |
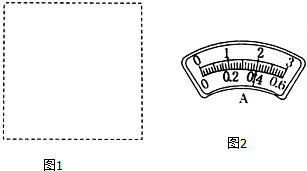 某物理“科技制作”小组装配一台小直流电动机,其额定电压5V,额定电流0.5A,线圈绕阻小于1Ω.为了进一步研究其在一定电压范围内,输出功率与输入电压的关系,需要进一步做实验,请你帮助该小组完成该项工作.已知学校实验室提供的器材有:
某物理“科技制作”小组装配一台小直流电动机,其额定电压5V,额定电流0.5A,线圈绕阻小于1Ω.为了进一步研究其在一定电压范围内,输出功率与输入电压的关系,需要进一步做实验,请你帮助该小组完成该项工作.已知学校实验室提供的器材有:
 如图为某电场的部分电场线.如A、B两点的场强分别记为EA、EB,电势分别记为φA、φB,则EA大于EB,φA小于φB.(选填“大于”、“小于”或“等于”).
如图为某电场的部分电场线.如A、B两点的场强分别记为EA、EB,电势分别记为φA、φB,则EA大于EB,φA小于φB.(选填“大于”、“小于”或“等于”). 如图所示,在真空中竖直平面内建立的xOy坐标系的第二象限中,有一个紧靠y轴且极板与x轴重合的平行板电容器,电容器上极板带正电、下极板带负电;y轴右侧有一以(R,0)为圆心、R为半径的圆形匀强磁场区域,磁场的磁感应强度大小为B、方向垂直于纸面向里;在y=R的上方足够大的范围内,有电场强度大小为E、方向水平向左的匀强电场.一质子(不计重力)从电容器左侧两级板正中间平行x轴方向射入,恰好从坐标原点O沿x轴正方向斜向下成30°方向射入磁场,经过一段时间后由P点穿出磁场,最后由M点(P点和M点没有在图中标出)穿出y轴.已知质子在磁场中做匀速圆周运动的半径也为R,质子的电荷量为e、质量为m.求;
如图所示,在真空中竖直平面内建立的xOy坐标系的第二象限中,有一个紧靠y轴且极板与x轴重合的平行板电容器,电容器上极板带正电、下极板带负电;y轴右侧有一以(R,0)为圆心、R为半径的圆形匀强磁场区域,磁场的磁感应强度大小为B、方向垂直于纸面向里;在y=R的上方足够大的范围内,有电场强度大小为E、方向水平向左的匀强电场.一质子(不计重力)从电容器左侧两级板正中间平行x轴方向射入,恰好从坐标原点O沿x轴正方向斜向下成30°方向射入磁场,经过一段时间后由P点穿出磁场,最后由M点(P点和M点没有在图中标出)穿出y轴.已知质子在磁场中做匀速圆周运动的半径也为R,质子的电荷量为e、质量为m.求;