题目内容
16. 如图所示,ABCD是一玻璃砖的截面图,一束光与AB面成30°角从AB边上的E点射入玻璃砖中,折射后经玻璃砖的BC边反射后,从CD边上的F点垂直于CD边射出.已知∠B=90°,∠C=60°,EB=10cm,BC=30cm.真空中的光速c=3×108m/s,求:
如图所示,ABCD是一玻璃砖的截面图,一束光与AB面成30°角从AB边上的E点射入玻璃砖中,折射后经玻璃砖的BC边反射后,从CD边上的F点垂直于CD边射出.已知∠B=90°,∠C=60°,EB=10cm,BC=30cm.真空中的光速c=3×108m/s,求:①玻璃砖的折射率;
②光在玻璃砖中从E到F所用的时间.(结果保留两位有效数字)
分析 ①根据题意作出光路图,由光的反射定律和几何知识求出入射角和折射角,再得到玻璃砖的折射率;
②根据几何知识求出光在玻璃砖中传播的距离,由v=$\frac{c}{n}$求出光在玻璃中传播的速度,从而求得传播的时间.
解答  解:①光在三棱镜中传播的光路如图所示,由几何关系可得:
解:①光在三棱镜中传播的光路如图所示,由几何关系可得:
i=60°,r=∠BQE=∠CQF=30°
由折射定律得:
n=$\frac{sini}{sinr}$=$\frac{sin60°}{sin30°}$=$\sqrt{3}$;
②由v=$\frac{c}{n}$,得 光在玻璃中传播的速度 v=$\sqrt{3}$×108m/s;
由几何关系得 $\overline{EQ}$=2$\overline{EB}$=20cm
$\overline{QF}$=$\overline{QC}$cos30°=($\overline{BC}$-$\overline{BQ}$)cos30°=(15$\sqrt{3}$-15)cm
则光在玻璃砖中从E到F所用的时间 t=$\frac{\overline{EQ}+\overline{QF}}{v}$=1.8×10-9s
答:光在玻璃砖中从E到F所用的时间是1.8×10-9s.
点评 此题关键是根据光的反射定律求解出各个分界面上的反射角和折射角,并结合几何关系进行分析计算.

练习册系列答案
相关题目
11.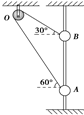 如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则杆对A、B的弹力之比为( )
如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则杆对A、B的弹力之比为( )
 如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则杆对A、B的弹力之比为( )
如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则杆对A、B的弹力之比为( )| A. | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{1}$ | B. | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{3}$ | C. | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{2}$ | D. | $\frac{{N}_{A}}{{N}_{B}}=\frac{2}{\sqrt{3}}$ |
1. 质量为0.2kg的物体在xoy平面上运动,其速度在x、y方向的分量vx、vy与时间t的关系如图所示,已知x、y方向相互垂直,则( )
质量为0.2kg的物体在xoy平面上运动,其速度在x、y方向的分量vx、vy与时间t的关系如图所示,已知x、y方向相互垂直,则( )
 质量为0.2kg的物体在xoy平面上运动,其速度在x、y方向的分量vx、vy与时间t的关系如图所示,已知x、y方向相互垂直,则( )
质量为0.2kg的物体在xoy平面上运动,其速度在x、y方向的分量vx、vy与时间t的关系如图所示,已知x、y方向相互垂直,则( )| A. | 0~4s内物体做曲线运动 | B. | 0~6s内物体一直做曲线运动 | ||
| C. | 0~4s内物体的位移为12m | D. | 4~6s内物体的位移为$\sqrt{5}$m |
8.用实验验证电磁波存在的科学家是( )
| A. | 法拉第 | B. | 奥斯特 | C. | 赫兹 | D. | 麦克斯韦 |
5.下列说法正确的是( )
| A. | 哥白尼提出了地心说 | B. | 牛顿发现了万有引力定律 | ||
| C. | 卡文迪许第一次测出了引力常量 | D. | 海王星被称为“笔尖下发现的行星” |
6.下列说法正确的是( )
| A. | $\left.\begin{array}{l}{210}\\{83}\end{array}\right.$Bi的半衰期是5天,12g$\left.\begin{array}{l}{210}\\{83}\end{array}\right.$Bi经过15天后还有1.5g为衰变 | |
| B. | 一束光照射到某种金属上不能发生光电效应,可能因为这束光的强度太小 | |
| C. | 机场、车站等地方进行安检工作时,能轻而易举地窥见箱内物品,利用了γ射线较强的穿透能力 | |
| D. | 处于基态的氢原子吸收一个光子跃迁到激发态,再向低能级跃迁时辐射光子的频率一定不大于入射光子的频率 | |
| E. | 铀($\left.\begin{array}{l}{238}\\{92}\end{array}\right.$U)经过多次α、β衰变形成稳定的铅$\left.\begin{array}{l}{206}\\{82}\end{array}\right.$Pb的过程中,有6个中子转变成质子 |
 如图,质量为1kg的小车A上用长的轻绳悬挂着质量为2kg的小球B,两者一起以4m/s的速度沿光滑水平面向右匀速运动,某一时刻,小车A与静止在水平面上的质量为1kg的形成C发生正碰并粘连在一起.重力加速度取10m/s2.求:
如图,质量为1kg的小车A上用长的轻绳悬挂着质量为2kg的小球B,两者一起以4m/s的速度沿光滑水平面向右匀速运动,某一时刻,小车A与静止在水平面上的质量为1kg的形成C发生正碰并粘连在一起.重力加速度取10m/s2.求: 如图所示,先将一端开口一端封闭,内径均匀,长度为L=100cm的玻璃管放在空气中,然后保持玻璃管竖直,把开口端向下缓慢插入水银槽中,水银进入玻璃管中,直到玻璃管内气柱长度变为L=95cm,已知大气压强p0=75cmHg,整个过程温度保持不变,求:此时玻璃管口距离水银液面的深度h.(结果保留两位有效数字)
如图所示,先将一端开口一端封闭,内径均匀,长度为L=100cm的玻璃管放在空气中,然后保持玻璃管竖直,把开口端向下缓慢插入水银槽中,水银进入玻璃管中,直到玻璃管内气柱长度变为L=95cm,已知大气压强p0=75cmHg,整个过程温度保持不变,求:此时玻璃管口距离水银液面的深度h.(结果保留两位有效数字) 如图所示,交流发电机内阻不计,它通过一个小灯泡L连接变压器,变压器输出并联24只相同的小灯泡L,每只灯泡都是“6V 0.25W”,所有灯泡都正常发光,导线电阻不计,求:
如图所示,交流发电机内阻不计,它通过一个小灯泡L连接变压器,变压器输出并联24只相同的小灯泡L,每只灯泡都是“6V 0.25W”,所有灯泡都正常发光,导线电阻不计,求: