��Ŀ����
19��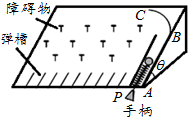 ��ͼ��ʾ����һ��ͯ��Ϸ���Ĺ���ʾ��ͼ����Ϸ���Ĺ⻬�����ˮƽ���һ�нǦȣ��뾶ΪR���ķ�֮һԲ�����BC��AB�ܵ�������B�㣬C��ΪԲ�������ߵ㣬�ᵯ���¶˹̶���AB�ܵ��ĵˣ��϶�ϵһ��������ͨ�������ڲ���һ�ֱ�P������Ͷ��AB���ڣ����������ֱ�ʹ���ɱ�ѹ�����ͷ��ֱ������鱻����������Ϸ����ڵ��ϰ����һϵ����ײ�����뵯����������������Ի�ò�ͬ�Ľ������������й�����⻬�����Կ����������������Ϊ�ʵ㣮ij�λ��������ֱ���ʹ�����B��ΪL���ͷ��ֱ������鱻����������C��ʱ�ٶ�Ϊv������˵����ȷ���ǣ�������
��ͼ��ʾ����һ��ͯ��Ϸ���Ĺ���ʾ��ͼ����Ϸ���Ĺ⻬�����ˮƽ���һ�нǦȣ��뾶ΪR���ķ�֮һԲ�����BC��AB�ܵ�������B�㣬C��ΪԲ�������ߵ㣬�ᵯ���¶˹̶���AB�ܵ��ĵˣ��϶�ϵһ��������ͨ�������ڲ���һ�ֱ�P������Ͷ��AB���ڣ����������ֱ�ʹ���ɱ�ѹ�����ͷ��ֱ������鱻����������Ϸ����ڵ��ϰ����һϵ����ײ�����뵯����������������Ի�ò�ͬ�Ľ������������й�����⻬�����Կ����������������Ϊ�ʵ㣮ij�λ��������ֱ���ʹ�����B��ΪL���ͷ��ֱ������鱻����������C��ʱ�ٶ�Ϊv������˵����ȷ���ǣ�������| A�� | ������ͷ��ֱ���ʼ�������ϰ���֮ǰ�Ĺ����л�е���غ� | |
| B�� | �˹����У����ɵ����������Ϊmg��L+R�� sin��+$\frac{1}{2}$mv2 | |
| C�� | �������뵯�ɵ�˲�䣬�䶯�ܺ���������֮�ʹﵽ��� | |
| D�� | �����ֱ���λ��ʹL�仯������ʹ�����C���뿪�����ȱ���ֱ���˶���ֱ�������ϰ��� |
���� ��е���غ��������ֻ���������������ݵ��������������������˶���������ݵ���͵�����ɵ�ϵͳ��е���غ㣬�������ܺ���������֮�ͺ�ʱ������ݻ�е���غ��ɵ���������ܣ�
��� �⣺A��������ͷ��ֱ��Ĺ��̣����ɶԵ��������������е�����ӣ���A����
B������ϵͳ�Ļ�е���غ�ã����ɵ���������ܵ��ڵ�����C��Ļ�е�ܣ�Ϊmg��L+R��sin��+$\frac{1}{2}$mv2����B��ȷ��
C��������ͷ��ֱ��Ĺ��̣����ɵĵ����Ե���������������Ķ��ܺ���������֮�Ͳ��������ݵ���͵�����ɵ�ϵͳ��е���غ㣬֪�������뵯�ɵ�˲�䣬���ɵĵ�������ȫ��ת��Ϊ����Ķ��ܺ��������ܣ����Դ�˲�䶯�ܺ���������֮�ʹﵽ���C��ȷ��
D�������C���뿪����ٶ�ˮƽ����������������б�����µķ��������ߴ�ֱ�����Ե������ȱ��������˶���ֱ�������ϰ����D����
��ѡ��BC
���� �������Ĺؼ�Ҫ֪������Ļ�е�ܲ��غ㣬����͵�����ɵ�ϵͳ��е�ܲ��غ㣬��ϵͳ���û�е���غ�����������⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
9��һ�п����г���72km/h���ٶ���һƽֱ��·�˶�����ʻԱ������ǰ����һ��ͯ����һͷţվ����������ˣ������ɲ����ɲ�����г��Դ�СΪ0.4m/s2�ļ��ٶȼ����˶���ǡ��û�������������Լ�ʻԱ�ķ�Ӧʱ�䣬��Մx��ʱ�г�����ͯ��ľ���Ϊ��������
| A�� | 250 m | B�� | 500 m | C�� | 750 m | D�� | 1000 m |
14������š����˷ɴ��롰�칬һ�š��ɹ��ԽӼ�������������DZͻ��7000����ѡ2012���й�ʮ��Ƽ���չ���ţ�������뾶ΪR���ѵ����������ֲ����ȵ����壨�����ֲ����ȵ���Ƕ�������һ�ʵ����������Ϊ�㣩��������������DZ���Ϊd�����칬һ�š�����������߶�Ϊh���������������ڴ��롰�칬һ�š����ڴ����������ٶ�֮��Ϊ��������
| A�� | $\frac{R-d}{R+h}$ | B�� | $\frac{��R-d��^{2}}{��R+h��^{2}}$ | C�� | $\frac{��R-d����R+h��^{2}}{{R}^{3}}$ | D�� | $\frac{��R-d����R+h��}{{R}^{2}}$ |
6�� ��ͼ��ʾ��һб��̶���ˮƽ���ϣ�б���ϵ�CD���ֹ⻬��DE���ֲִڣ�A��B�����������һ�𣬴Ӷ���C���ɾ�ֹ�»����»�������A��B������Ծ�ֹ������DE���������˶�����֪A��B��ĽӴ���ˮƽ��������
��ͼ��ʾ��һб��̶���ˮƽ���ϣ�б���ϵ�CD���ֹ⻬��DE���ֲִڣ�A��B�����������һ�𣬴Ӷ���C���ɾ�ֹ�»����»�������A��B������Ծ�ֹ������DE���������˶�����֪A��B��ĽӴ���ˮƽ��������
 ��ͼ��ʾ��һб��̶���ˮƽ���ϣ�б���ϵ�CD���ֹ⻬��DE���ֲִڣ�A��B�����������һ�𣬴Ӷ���C���ɾ�ֹ�»����»�������A��B������Ծ�ֹ������DE���������˶�����֪A��B��ĽӴ���ˮƽ��������
��ͼ��ʾ��һб��̶���ˮƽ���ϣ�б���ϵ�CD���ֹ⻬��DE���ֲִڣ�A��B�����������һ�𣬴Ӷ���C���ɾ�ֹ�»����»�������A��B������Ծ�ֹ������DE���������˶�����֪A��B��ĽӴ���ˮƽ��������| A�� | ��CD�����»�ʱ��A�Ļ�е�ܼ�С��B�Ļ�е�����ӣ����ܵĻ�е�ܲ��� | |
| B�� | ��CD�����»�ʱ��A�Ļ�е�����ӣ�B�Ļ�е�ܼ�С�����ܵĻ�е�ܲ��� | |
| C�� | ��DE�����»�ʱ��A�Ļ�е�ܲ��䣬B�Ļ�е�ܼ�С�����ܵĻ�е�ܼ�С | |
| D�� | ��DE�����»�ʱ��A�Ļ�е�ܼ�С��B�Ļ�е�ܼ�С�����ܵĻ�е�ܼ�С |
3������ļ����ٶ��б�ʾ˲ʱ�ٶȵ��ǣ�������
| A�� | �ӵ����ǹ�ڵ��ٶ���800 m/s���� 790 m/s���ٶȻ���Ŀ�� | |
| B�� | �����Ӽ�վ��ʻ����վ�����е��ٶ���40 km/h | |
| C�� | ����ͨ��վ��ʱ���ٶ���72 km/h | |
| D�� | С���3 sĩ���ٶ���6 m/s |
4��һ�����������˷ֱ�˩����С��һ��������ס�϶˵�һ�������Ǵ���¥��̨���ɾ�ֹ�ͷţ������Ⱥ���ص�ʱ���Ϊ��t1���������Ǵ���¥��̨���ɾ�ֹ�ͷţ���������ص�ʱ���Ϊ��t2�����ƿ������������t1����t2���㣨������
| A�� | ��t1=��t2 | B�� | ��t1����t2 | C�� | ��t1����t2 | D�� | ���϶��п��� |
 �軬ѩ�˶�Ա��a����ˮƽ��������̨������һ��ʱ��ķ��У���b����أ�a��b����ֱ�߾���Ϊ40m��ab������ˮƽ�����30��ǣ���ͼ��ʾ�����ƿ�����������
�軬ѩ�˶�Ա��a����ˮƽ��������̨������һ��ʱ��ķ��У���b����أ�a��b����ֱ�߾���Ϊ40m��ab������ˮƽ�����30��ǣ���ͼ��ʾ�����ƿ����������� Ϊ�˲ⶨһ��صĵ綯�ƣ�Լ6V�����ڵ��裬ʵ�������ṩ���������ģ�
Ϊ�˲ⶨһ��صĵ綯�ƣ�Լ6V�����ڵ��裬ʵ�������ṩ���������ģ�