题目内容
10.关于万有引力定律,下列说法正确的有( )| A. | 关于公式$\frac{{R}^{3}}{{T}^{2}}$=k中的常量k,它是一个与中心天体有关的常量 | |
| B. | 开普勒定律,只适用于太阳系,对其他恒星系不适用 | |
| C. | 已知金星绕太阳公转的周期小于地球绕太阳公转的周期,则可判定金星到太阳的距离小于地球到太阳的距离 | |
| D. | 发现万有引力定律和测出引力常量的科学家分别是开普勒、伽利略 | |
| E. | 两个靠近的天体绕同一点运动称为双星,如图所示,则两星球的轨道半径与二者的质量成反比 |
分析 开普勒第三定律$\frac{{R}_{\;}^{3}}{{T}_{\;}^{2}}$=k中,与中心天体有关的常量;根据行星公转时万有引力提供圆周运动的向心力,$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$展开讨论即可.
解答 解:A、开普勒第三定律$\frac{{R}_{\;}^{3}}{{T}_{\;}^{2}}$=k中,k是一个与中心天体有关的常量,故A正确
B、开普勒定律,也适用于太阳系,对其他恒星系也适用;行星的卫星(包括人造卫星)绕行星的运动,是遵循开普勒定律的,故B错误;
C、根据开普勒第三定律$\frac{{R}_{\;}^{3}}{{T}_{\;}^{2}}=k$,由题金星绕太阳公转的周期小于地球绕太阳公转的周期,则金星到太阳的距离小于地球到太阳的距离.故C正确;
D、牛顿发现万有引力定律,卡文迪许测出引力常量的科学家,故D错误;
E、在双星问题中它们的角速度相等,设两星之间的距离为L,则有:$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}{ω}_{\;}^{2}{r}_{1}^{\;}={m}_{2}^{\;}{ω}_{\;}^{2}{r}_{2}^{\;}$,可得:m1r1=m2r2,即轨道半径和质量成反比,故E正确;
故选:ACE
点评 本题行星运动模型与卫星绕地球运动模型相似,抓住由中心天体的万有引力提供向心力,列方程分析各物理量的关系.注意双星问题中两卫星的向心力相同,角速度相等.

练习册系列答案
相关题目
1.某个行星的质量是地球质量的一半,半径也是地球半径的一半.某运动员在地球上能举起250kg的杠铃,在该行星上最多能举起质量为多少的杠铃( )
| A. | 50kg | B. | 125kg | C. | 250kg | D. | 500kg |
18.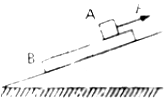 两个物块A、B叠放在光滑的斜面上,用方向与斜面平行的拉力F作用在A上,使两物块一起沿斜面向上做匀速运动,则下列说法中正确的有( )
两个物块A、B叠放在光滑的斜面上,用方向与斜面平行的拉力F作用在A上,使两物块一起沿斜面向上做匀速运动,则下列说法中正确的有( )
 两个物块A、B叠放在光滑的斜面上,用方向与斜面平行的拉力F作用在A上,使两物块一起沿斜面向上做匀速运动,则下列说法中正确的有( )
两个物块A、B叠放在光滑的斜面上,用方向与斜面平行的拉力F作用在A上,使两物块一起沿斜面向上做匀速运动,则下列说法中正确的有( )| A. | 物块B受到A的静摩擦力沿斜面向上 | B. | 物块B给A的静摩擦力沿斜面向上 | ||
| C. | 物块A所受到的静摩擦力大小等于F | D. | 物块A所受到的静摩擦力大小小于F |
5.关于匀变速直线运动中加速度的正负,下列说法中正确的是( )
| A. | 匀加速直线运动中,加速度一定是正值 | |
| B. | 匀减速直线运动中,加速度一定是负值 | |
| C. | 只有在规定了初速度方向为正方向的前提下,匀加速直线运动加速度才取正值 | |
| D. | 以上说法都不对 |
15.一辆车以速度v行驶了一半的路程,接着以20km/h的速度跑完了余下的路程,若全程的平均速度是24km/h,则v是( )
| A. | 28 km/h | B. | 30km/h | C. | 22 km/h | D. | 44km/h |
2.在电场中某点放一检验电荷,其电量为q,检验电荷受到的电场力为F,则该点电场强度为E=$\frac{F}{q}$,那么下列说法正确的是( )
| A. | 若移去检验电荷q,该点的电场强度就变为零? | |
| B. | 若在该点放一个电量为2q的检验电荷,该点的场强就变为$\frac{E}{2}$ | |
| C. | 若在该点放一个电量为-2q的检验电荷,则该点场强大小仍为E,但电场强度的方向变为原来相反的方向? | |
| D. | 若在该点放一个电量为-q的检验电荷,则该点的场强大小仍为E,电场强度的方向也还是原来的场强方向? |
19. 如图所示,直线A为电源a的路端电压与电流的关系图线;直线B为电源b的路端电压与电流的关系图线;直线C为一个电阻R两端电压与电流的关系图线.将这个电阻分别接到a、b两电源上,那么( )
如图所示,直线A为电源a的路端电压与电流的关系图线;直线B为电源b的路端电压与电流的关系图线;直线C为一个电阻R两端电压与电流的关系图线.将这个电阻分别接到a、b两电源上,那么( )
 如图所示,直线A为电源a的路端电压与电流的关系图线;直线B为电源b的路端电压与电流的关系图线;直线C为一个电阻R两端电压与电流的关系图线.将这个电阻分别接到a、b两电源上,那么( )
如图所示,直线A为电源a的路端电压与电流的关系图线;直线B为电源b的路端电压与电流的关系图线;直线C为一个电阻R两端电压与电流的关系图线.将这个电阻分别接到a、b两电源上,那么( )| A. | 电源a的内阻更大 | |
| B. | 电源b的电动势更大 | |
| C. | R接到a电源上时,电源的输出功率更大 | |
| D. | R接到a电源上时,电源效率更高 |
20.关于伽利略对自由落体运动的研究,下列说法正确的是( )
| A. | 伽利略猜想运动速度与下落的时间成正比,并直接用实验进行了验证 | |
| B. | 伽利略通过数学推演并用小球在斜面上验证了位移与时间成正比 | |
| C. | 伽利略思想方法的核心是把实验和逻辑推理(包括数学推演)和谐的结合起来 | |
| D. | 伽利略直接通过实验验证了自由落体运动位移与时间二次方成正比 |
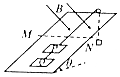 如图所示,光滑固定斜面倾角为θ=37°,斜面上有两个完全相同的正方形线框P、Q用细线连接,P通过平行于斜面的细线绕过斜面顶端的定滑轮与一重物相连接,开始重物固定,线框处于静止,斜面上水平虚线MN上方有垂直于斜面向下的匀强磁场,磁感应强度大小为B,线框的边长及P线框最上边到MN的距离均为L,释放重物,使重物带动线框沿斜面向上运动,两个线框的质量均为m,每个线框的电阻均为R,重物的质量为2m,虚线上方的斜面足够长,重物离地面足够高,线框运动过程中,上边始终与MN平行,重力加速度为g,当线框P刚好要完全进入磁场的一瞬间,重物的加速度为零,sin37°=0.6,cos37°=0.8,求:
如图所示,光滑固定斜面倾角为θ=37°,斜面上有两个完全相同的正方形线框P、Q用细线连接,P通过平行于斜面的细线绕过斜面顶端的定滑轮与一重物相连接,开始重物固定,线框处于静止,斜面上水平虚线MN上方有垂直于斜面向下的匀强磁场,磁感应强度大小为B,线框的边长及P线框最上边到MN的距离均为L,释放重物,使重物带动线框沿斜面向上运动,两个线框的质量均为m,每个线框的电阻均为R,重物的质量为2m,虚线上方的斜面足够长,重物离地面足够高,线框运动过程中,上边始终与MN平行,重力加速度为g,当线框P刚好要完全进入磁场的一瞬间,重物的加速度为零,sin37°=0.6,cos37°=0.8,求: