题目内容
9. 一根长为L的杆OA,O端用铰链固定,另一端固定着一个小球A,靠在一个质量为M,高为h的物块上,如图所示,若物块与地面摩擦不计,试求当物块以速度v向右运动时,小球A的线速度vA(此时杆与水平方向夹角为θ).
一根长为L的杆OA,O端用铰链固定,另一端固定着一个小球A,靠在一个质量为M,高为h的物块上,如图所示,若物块与地面摩擦不计,试求当物块以速度v向右运动时,小球A的线速度vA(此时杆与水平方向夹角为θ).
分析 将物块的速度分解为沿杆子方向和垂直于杆子方向,在垂直于杆子方向上的速度等于B点绕O转动的线速度,根据v=rω可求出杆转动的角速度,再根据杆的角速度和A的转动半径可以求出A的线速度大小.
解答 解:将B点的速度分解如图所示
根据运动的合成与分解可知,接触点B的实际运动为合运动,可将B点运动的速度vB=v沿垂直于杆和沿杆的方向分解成v2和v1,其中v2=vBsinθ=vsinθ为B点做圆周运动的线速度,v1=vBcosθ为B点沿杆运动的速度.当杆与水平方向夹角为θ时,OB=$\frac{h}{sinθ}$
由于B点的线速度为v2=vsinθ=$\overline{OB}•$ω,所以$ω=\frac{vsinθ}{OB}$=$\frac{vsi{n}^{2}θ}{h}$;
由于A、B在同一杆上绕O点做圆周运动,故A、B绕O做圆周运动的角速度相同;所以A的线速度vA=Lω=$\frac{Lvsi{n}^{2}θ}{h}$.
答:小球A的线速度vA是$\frac{Lvsi{n}^{2}θ}{h}$.
点评 解决本题的关键会根据平行四边形定则对速度进行分解,木块速度在垂直于杆子方向的分速度等于B点转动的线速度.

练习册系列答案
相关题目
1.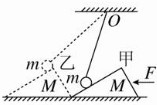 如图所示,小球m用一条不可伸长的轻质细线拴住后悬于O点,小球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置甲向左缓慢移动到位置乙,在此过程中,正确的说法是( )
如图所示,小球m用一条不可伸长的轻质细线拴住后悬于O点,小球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置甲向左缓慢移动到位置乙,在此过程中,正确的说法是( )
 如图所示,小球m用一条不可伸长的轻质细线拴住后悬于O点,小球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置甲向左缓慢移动到位置乙,在此过程中,正确的说法是( )
如图所示,小球m用一条不可伸长的轻质细线拴住后悬于O点,小球置于一个斜面不光滑的斜劈M上,用水平力F向左推动斜劈M在光滑水平桌面上由位置甲向左缓慢移动到位置乙,在此过程中,正确的说法是( )| A. | M、m间的摩擦力对m不做功 | |
| B. | M、m间的摩擦力对m做负功 | |
| C. | F对M所做的功与m对M所做的功的绝对值相等 | |
| D. | M、m间的弹力对m做正功 |
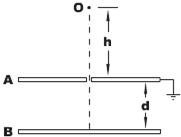 如图所示,水平放置的两平行金属板A、B构成电容器,电容为C,极板间距为d,开始时两板均不带电,让带有小孔的A板接地.在A板小孔的正上方高h的O点有带电油滴一滴一滴地滴下,已知油滴每滴的质量为m,电量为q,且每滴落到B板后,都会将电荷全部传给B板(A板的下表面也会同时感应出等量的异种电荷),空气阻力不计.求:
如图所示,水平放置的两平行金属板A、B构成电容器,电容为C,极板间距为d,开始时两板均不带电,让带有小孔的A板接地.在A板小孔的正上方高h的O点有带电油滴一滴一滴地滴下,已知油滴每滴的质量为m,电量为q,且每滴落到B板后,都会将电荷全部传给B板(A板的下表面也会同时感应出等量的异种电荷),空气阻力不计.求: 如图,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10米,BC长1米,AB和CD轨道光滑.一质量为1千克的物体,从A点以4米/秒的速度开始运动,经过BC后滑到高出C点10.3m的D点速度为零.求:(g=10m/s2)
如图,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10米,BC长1米,AB和CD轨道光滑.一质量为1千克的物体,从A点以4米/秒的速度开始运动,经过BC后滑到高出C点10.3m的D点速度为零.求:(g=10m/s2)