��Ŀ����
16�� ijͬѧ����ͼʾװ�ã���֤�����������ɣ�
ijͬѧ����ͼʾװ�ã���֤�����������ɣ��������ͨ�������쳤��ϸ�������ӣ��������ٶ���ȣ�
��ϵͳ��е���غ㣮
P��Q��R��������ȫ��ͬ����飬P��Q��ϸ�����ӣ�����ˮƽ�������ϣ����R���Ử�����ӣ��������м䣬a��b��c����������ţ�������������ŵ�λ�ã���ʵ��ͬʱ�ڹ⣬����װ�����ٶ��ͷţ�
��1��Ϊ�������ʵ��Ŀ�ģ����˼�¼P��Q��R�����ڹ�Ƭ���ڹ�ʱ��t1��t2��t3�⣬�������������������BCD��
A��P��Q��R������M B�����������ֵľ���d
C��R���ڹ�Ƭ��c�ľ���H D���ڹ�Ƭ�Ŀ���x
��2������װ�ÿ��Է�����P��Q���ٶȴ�С��ȣ���֤����ʽΪt1=t2��
��3����Ҫ��֤���R�����P���������ٶ���ȣ�����֤����ʽΪ$\frac{{t}_{3}}{{t}_{1}}=\frac{2H}{\sqrt{4{H}^{2}+{d}^{2}}}$��
��4������֪�����������ٶ�g������֤ϵͳ��е���غ�ı���ʽΪgH=$\frac{1}{2}{x}^{2}��\frac{1}{{t}_{1}^{2}}+\frac{1}{{t}_{2}^{2}}+\frac{1}{{t}_{3}^{2}}��$��
���� ��1��������֤ϵͳ��е���غ���Ҫ��֤�ı���ʽ���ҳ���Ҫ��������������
��2���ֱ����P��Q���ٶȴ�С���ٸ����������ٶ���ȣ������Ҫ��֤�ı���ʽ��
��3���ֱ����P��R���ٶȴ�С���ٸ����������ٶ���ȣ������Ҫ��֤�ı���ʽ��
��4�����ݻ�е���غ㶨����ʽ�����������֤ϵͳ��е���غ�ı���ʽ��
��� �⣺��1��Ҫ֤���٣���Ҫ����d��H��ͨ�����ι�ϵ��֤���������ٶ���ȣ�Ҫ֤���ڣ�����Ҫ����H��x�������˶�ѧ��ʽ�Ͷ��ܶ�����ʽ����֤��е���غ㣬����Ҫ��������������d��H��x����BCD��ȷ��
��ѡ��BCD��
��2�����P���ٶ�${v}_{P}=\frac{x}{{t}_{1}}$�����Q���ٶ�${v}_{Q}=\frac{x}{{t}_{2}}$����˷�����P��Q���ٶȴ�С��ȣ�����Ҫ��֤����ʽ$\frac{x}{{t}_{1}}=\frac{x}{{t}_{2}}$������ɵ���֤t1=t2���ɣ�
��3�����R���ٶ�${v}_{R}=\frac{x}{{t}_{3}}$��Ҫ��֤���R�����P���������ٶ���ȣ�����Ҫ��֤����ʽ$\frac{{t}_{3}}{{t}_{1}}=\frac{2H}{\sqrt{4{H}^{2}+{d}^{2}}}$��
��4������ϵͳ���ٵĻ�е���ǡ�E=MgH�����ӵĻ�е����$��{E}^{��}=\frac{1}{2}M{v}_{P}^{2}+\frac{1}{2}M{v}_{Q}^{2}+\frac{1}{2}M{v}_{R}^{2}$
Ҫ��֤��е���غ㣬���E=��E�䣬����֤����ʽgH=$\frac{1}{2}{x}^{2}��\frac{1}{{t}_{1}^{2}}+\frac{1}{{t}_{2}^{2}}+\frac{1}{{t}_{3}^{2}}��$��
�ʴ�Ϊ����1��BCD����2��t1=t2����3��$\frac{{t}_{3}}{{t}_{1}}=\frac{2H}{\sqrt{4{H}^{2}+{d}^{2}}}$����4��gH=$\frac{1}{2}{x}^{2}��\frac{1}{{t}_{1}^{2}}+\frac{1}{{t}_{2}^{2}}+\frac{1}{{t}_{3}^{2}}��$��
���� ���⿼������֤��е���غ㶨�ɵ�ʵ�飬����Ĺؼ�����ȷʵ��ԭ�����ҳ���������֮��Ĺ�ϵ���ٽ�ϻ�е���غ㶨��д����Ҫ��֤�ı���ʽ��

 ����ܵĹ���ԭ��ͼ��ͼ��ʾ��ͼ����Ӱ����û�дų�ʱ���ӵ���ǹ�����ĵ��Ӵ���ӫ�������е�O�㣮Ϊʹ��������ֱ����ƫ�����ģ�����ӫ�����ϵ�A�㣬��Ӱ�������Ӵų��ķ����ǣ�������
����ܵĹ���ԭ��ͼ��ͼ��ʾ��ͼ����Ӱ����û�дų�ʱ���ӵ���ǹ�����ĵ��Ӵ���ӫ�������е�O�㣮Ϊʹ��������ֱ����ƫ�����ģ�����ӫ�����ϵ�A�㣬��Ӱ�������Ӵų��ķ����ǣ�������| A�� | ��ֱ���� | B�� | ��ֱ���� | C�� | ��ֱ��ֽ������ | D�� | ��ֱ��ֽ������ |
| A�� | �����ܵ������� | B�� | �������ܵ������� | ||
| C�� | ����α� | D�� | ������α� |
| A�� |  ��ͼ��ֱ����ˮͰ��ˮƽ����������ǰ�� | |
| B�� |  ��ͼ�����״���������¥�� | |
| C�� |  ��ͼ����������������û�� | |
| D�� |  ��ͼ���Ÿ���ԭ�ز��� |
| t/s | 0 | 1 | 2 | 3 | 4 |
| x/m | 0 | 5 | -4 | -1 | -7 |
| A�� | ��4s�ڵ�λ����� | B�� | ǰ4s�ڵ�λ����� | ||
| C�� | ��2s�ڵ�·����� | D�� | ǰ2s�ڵ�·����� |
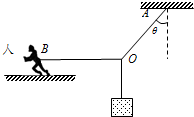 ��ͼ��ʾ�����ͨ��3���������ң�3�������Ľ��ΪO������OBˮƽ��B����վ��ˮƽ���ϵ�����Ϊm2=60kg��������������OA����ֱ����ļнǦ�=37�㣬��鼰�˶����ھ�ֹ״̬����֪����ˮƽ��֮��Ķ�Ħ������Ϊ��=0.3��sin37��=0.6��cos37��=0.8��ȡg=10m/s2�������Ħ�������ڻ���Ħ������Ҫ������ˮƽ���ϲ���������
��ͼ��ʾ�����ͨ��3���������ң�3�������Ľ��ΪO������OBˮƽ��B����վ��ˮƽ���ϵ�����Ϊm2=60kg��������������OA����ֱ����ļнǦ�=37�㣬��鼰�˶����ھ�ֹ״̬����֪����ˮƽ��֮��Ķ�Ħ������Ϊ��=0.3��sin37��=0.6��cos37��=0.8��ȡg=10m/s2�������Ħ�������ڻ���Ħ������Ҫ������ˮƽ���ϲ���������

 ͼΪ����֤ţ�ٵڶ����ɡ���ʵ��װ��ʾ��ͼ��ɰ��ɰͰ��������Ϊm��С���������������ΪM��ʵ������ɰ��ɰͰ�������Ĵ�С��Ϊϸ�߶�С�������Ĵ�С��
ͼΪ����֤ţ�ٵڶ����ɡ���ʵ��װ��ʾ��ͼ��ɰ��ɰͰ��������Ϊm��С���������������ΪM��ʵ������ɰ��ɰͰ�������Ĵ�С��Ϊϸ�߶�С�������Ĵ�С��