上海电信宽频私人用户月收费标准如下表
| 方案 | 类别 | 基本费用 | 超时费用 |
| 甲 | 包月制(不限时) | 130元 | 无 |
| 乙 | 有限包月制(限60小时) | 80元 | 3元/小时 |
1)某用户每月上网时间为70小时,应选择哪种方案
2)写出方案乙中每月总费用y(元)关于时间t(小时)的函数关系式
3)费先生一年内每月上网时间t(n)(小时)与月份n的函数为
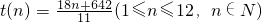 ,问费先生全年的上网费用最少为多少元?
,问费先生全年的上网费用最少为多少元? | 方案 | 类别 | 基本费用 | 超时费用 |
| 甲 | 包月制(不限时) | 130元 | 无 |
| 乙 | 有限包月制(限60小时) | 80元 | 3元/小时 |
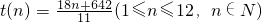 ,问费先生全年的上网费用最少为多少元?
,问费先生全年的上网费用最少为多少元?