观察下列等式：1³+2³=3²，1³+2³+3³=6²，1³+2³+3³+4³=10²，…，根据上述规律，第五个等式为

　　．

设函数f（x）=，则f[f（）]=　_．

某几何体的三视图如图所示，则这个几何体的体积是　_．

已知单位向量的夹角为60°，则=　_．

函数y=的定义域为　　．

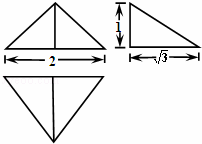
已知函数y=f（x）是定义在R上的奇函数，且当x∈（﹣∞，0）时不等式f（x）+xf′（x）＜0成立，若a=3^0.3•f（3^0.3），b=（log_π3）•f（log_π3），c=（）•f（）．则a，b，c的大小关系是（　　）

若x，y满足约束条件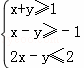目标函数z=ax+2y仅在点（1，0）处取得最小值，则a的取值范围是（　　）

如图，函数y=f（x）的图象为折线ABC，设g （x）=f[f（x）]，则函数y=g（x）的图象为（　　）

设函数f（x）=x³﹣4x+a，0＜a＜2．若f（x）的三个零点为x₁，x₂，x₃，且x₁＜x₂＜x₃，则（　　）

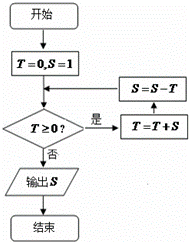
执行如图所示的程序框图，输出的S值为（　　）