(本小题满分12分)
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
| 分组 |
|
|
|
|
|
|
| [140,150] |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
乙校:
| 分组 |
|
|
|
|
|
|
| [140,150] |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(1)计算x,y的值,并分别估计两上学校数学成绩的优秀率;
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
附:![]()
|
| 0.10 | 0.025 | 0.010 |
|
| 2.706 | 5.024 | 6.635 |
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
由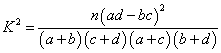 算得,
算得,![]() .
.
|
| 0.050 | 0.010 | 0.001 |
|
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是
A.再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
由![]() 算得,
算得,![]()
附表:
|
| 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是
A.有99%以上的把握认为“爱好该项运动与性别有关”
B.有99%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为 “爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为 “爱好该项运动与性别无关”
(本小题满分12分)
调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据:出生时间在晚上的男婴为24人,女婴为8人;出生时间在白天的男婴为31人,女婴为26人.
(1)将下面的2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系?
| 出生时间 性别 | 晚上 | 白天 | 合计 |
| 男婴 |
| ||
| 女婴 |
| ||
| 合计 |
|
|
|
| P(K2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
K2=![]()
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程![]() 必过(
必过(![]() );
);
④在一个2×2列联中,由计算得![]() 则有99%的把握确认这两个变量间有关系;其中错误的个数是 ( )
则有99%的把握确认这两个变量间有关系;其中错误的个数是 ( )
A.0 B.1 C.2 D.3
本题可以参考独立性检验临界值表:
|
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |