(本小题满分12分)某大学高等数学老师这学期分别用
(本小题满分12分)某大学高等数学老师这学期分别用![]() 两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:(Ⅰ)依茎叶图判断哪个班的平均分高?
两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
下面临界值表仅供参考:
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() 其中
其中![]() )
)
(本小题满分12分)
在“家电下乡”活动中,某品牌家电厂家从某地购买该品牌家电的用户中随机抽取20名用户进行满意度调查.设满意度最低为0,最高为10,抽查结果统计如下:
| 满意度分组 |
|
|
|
|
|
| 用户数 | 1 | 2 | 4 | 5 | 8 |
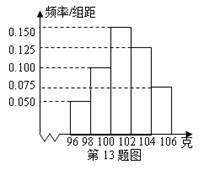
(1)完成下列频率分布直方图:

(2)估计这20名用户满意度的中位数(写出计算过程);
(3)设第四组(即满意度在区间![]() 内)的5名用户的满意度数据分别为:
内)的5名用户的满意度数据分别为:![]() ,先从中任取两名不同用户的满意度数据
,先从中任取两名不同用户的满意度数据![]() 、
、![]() ,求
,求![]() 的概率.
的概率.
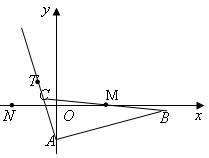 已知
已知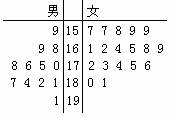 (2)若从所有“高个子”中选3名志愿者,用
(2)若从所有“高个子”中选3名志愿者,用