20.某商场在促销期间规定:商场内所有商品按标价的80%出售;同时, 当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额 (元)的范围 | [200,400) | [400,500) | [500,700) | [700,900] | … |
获得奖券 的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110元.
设购买商品得到的优惠率=![]() ,试问:
,试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不少于![]() 的优惠率?
的优惠率?
19.已知函数f(x)=x2+2x·tanθ-1,x∈[-1, ],其中θ∈(-
],其中θ∈(- ,
, ).
).
0 57811 57819 57825 57829 57835 57837 57841 57847 57849 57855 57861 57865 57867 57871 57877 57879 57885 57889 57891 57895 57897 57901 57903 57905 57906 57907 57909 57910 57911 57913 57915 57919 57921 57925 57927 57931 57937 57939 57945 57949 57951 57955 57961 57967 57969 57975 57979 57981 57987 57991 57997 58005 266669
(1)当θ=-![]() 时,求函数f(x)的最大值与最小值;
时,求函数f(x)的最大值与最小值;
(2)求θ的取值范围,使y=f(x)在区间[-1,![]() ]上是单调函数.
]上是单调函数.
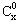 =1,这是组合数
=1,这是组合数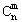 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.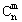 =C
=C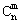 +C
+C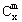 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.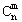 是正整数,证明:当x∈Z,m是正整数时,
是正整数,证明:当x∈Z,m是正整数时,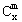 ∈Z
∈Z