题目内容
22.规定C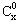
＝
，其中x∈R，m是正整数，且 
＝1，这是组合数
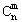（n、m是正整数，且m≤n）的一种推广.
（1）求C
的值；
（2）组合数的两个性质；
①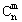
＝C
. ②
＋C
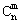＝C
.
是否都能推广到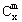
（x∈R，m是正整数）的情形？若能推广，则写出推广的形式并给出证明；若不能，则说明理由.
（3）已知组知数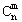
是正整数，证明：当x∈Z，m是正整数时，
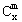∈Z
22.
［解］（1）C
＝
＝－C
＝－11628
（2）性质①不能推广，例如当x＝2时，C
有定义，但C
无意义；
性质②能推广，它的推广形式是C
＋C
＝C，x∈R，m是正整数，事实上
当m＝1时，有C＋C＝x＋1＝C，
当m≥2时，
C＋C＝
＝
＝
＝C
.
［证明］（3）当x≥m时，组合数C
∈Z.
当0≤x＜m时， C
＝0∈Z.
当x＜0时，∵－x＋m－1＞0，
∴C
＝
＝（－1）m 
＝（－1）mC
∈Z
练习册系列答案
智慧小复习系列答案
相关题目
其中P、M为实数集R的两个非空子集，又规定f(P)＝{y|y＝f(x)，x∈P}，f(M)＝{y|y＝f(x)，x∈M}．给出下列四个判断，其中正确判断有
，则f(P)∩f(M)＝
其中P，M为实数集R的两个非空子集，又规定f(P)＝{y|y＝f(x)，x∈P}，f(M)＝{y|y＝f(x)，x∈M}．给出下列四个判断：
，则f(P)∩f(M)＝
其中P、M为实数集R的两个非空子集，又规定f(P)＝{y|y＝f(x)，x∈P}，f(M)＝{y|y＝f(x)，x∈M}，给出下列四个判断：①若P∩M＝
，则f(P)∩f(M)＝
＝
，其中x∈R，m是正整数，且 C
＝1，
（n、m是正整数，且m≤n）的一种推广.
的值；
取得最小值？
＝C
. ②C
＋C
＝C
.
（x∈R，m是正整数）的情形？若能推广，则写出推广的形式并给出证明；若不能，则说明理由.