最近.某人准备将手中的10万块钱投资理财.现有二种方案:第一种方案:将10万块钱全部用来买股票.据分析预测:投资股市一年可能获利40%.也可能亏损20%.且获利的概率为12．第二种方案:将10万块钱全——青夏教育精英家教网——

最近，某人准备将手中的10万块钱投资理财，现有二种方案：第一种方案：将10万块钱全部用来买股票，据分析预测：投资股市一年可能获利40%，也可能亏损20%（只有这两种可能），且获利的概率为

．第二种方案：将10万块钱全部用来买基金，据分析预测：投资基金一年可能获利20%，也可能损失10%，也可能不赔不赚，且三种情况发生的概率分别为

．针对以上两种投资方案，请你为选择一种合理的理财方法，并说明理由．

某食品厂为了检查甲乙两条自动包装流水线的生产情况，随即在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．图1是甲流水线样本的频率分布直方图，表1是乙流水线样本频数分布表．

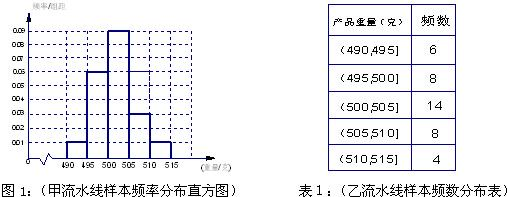
（1）若以频率作为概率，试估计从甲流水线上任取5件产品，求其中合格品的件数X的数学期望；
（2）从乙流水线样本的不合格品中任意取2件，求其中超过合格品重量的件数Y的分布列；
（3）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．

	甲流水线	乙流水线	合计
合格品	a=	b=
不合格品	c=	d=
合　计			n=

P（K²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

附：下面的临界值表供参考：
（参考公式：K2=

(a+b)(c+d)(a+c)(b+d)

，其中n=a+b+c+d）

)n二项展开式中，第4项的二项式系数与第3项的二项式系数的比为8：3．
（I）求n的值；
（II）求展开式中x³项的系数．

已知事件A发生的概率为0.5，事件B发生的概率为0.3，事件A和事件B同时发生的概率为0.2，则在事件A发生的条件下、事件B发生的概率为

设随机变量ξ服从正态分布N（u，9），若p（ξ＞3）=p（ξ＜1），则u=

设(1+x)n=a0+a1x+…+anxn，若a₁+a₂+…+a_n=63，则展开式中系数最大的项是（　　）

袋中装有6个不同的红球和4个不同的白球，不放回地依次摸出2个球，在第1次摸出红球的条件下，第2次摸出的也是红球的概率为（　　）

将7名学生分配到甲、乙两个宿舍，每个宿舍至少安排2名学生，那么互不相同的安排方法的种数为（　　）

n(n+1)(n+2)…(n+100)

可表示为（　　）

设函数f（x）=（x+1）ln（x+1）-ax在x=0处取得极值．
（1）求a的值及函数f（x）的单调区间；
（2）证明对任意的正整数n，不等式nlnn≥（n-1）ln（n+1）．

0 41224 41232 41238 41242 41248 41250 41254 41260 41262 41268 41274 41278 41280 41284 41290 41292 41298 41302 41304 41308 41310 41314 41316 41318 41319 41320 41322 41323 41324 41326 41328 41332 41334 41338 41340 41344 41350 41352 41358 41362 41364 41368 41374 41380 41382 41388 41392 41394 41400 41404 41410 41418 266669