已知双曲线
-
=1（a＞0）的离心率为2，则a=（ ）
| x2 |
| a2 |
| y2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、1 |
在一段时间内，甲去某地的概率是
，乙去此地的概率是
，假定两人的行动相互之间没有影响，那么在这段时间内至少有1人去此地的概率是（ ）
| 1 |
| 4 |
| 1 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，A地到火车站共有两条路径L1和L2，据统计，通过两条路径所用的时间互不影响，所用时间落在各时间段内的频率如下表：
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站．
（Ⅰ）为了尽最大可能在各自允许的时间内赶到火车站，甲和乙应如何选择各自的路径？
（Ⅱ）用X表示甲、乙两人中在允许的时间内能赶到火车站的人数，针对（Ⅰ）的选择方案，求X的分布列和数学期望．
0 32620 32628 32634 32638 32644 32646 32650 32656 32658 32664 32670 32674 32676 32680 32686 32688 32694 32698 32700 32704 32706 32710 32712 32714 32715 32716 32718 32719 32720 32722 32724 32728 32730 32734 32736 32740 32746 32748 32754 32758 32760 32764 32770 32776 32778 32784 32788 32790 32796 32800 32806 32814 266669
| 所用时间（分钟） | 10～20 | 20～30 | 30～40 | 40～50 | 50～60 |
| L1的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
| L2的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
（Ⅰ）为了尽最大可能在各自允许的时间内赶到火车站，甲和乙应如何选择各自的路径？
（Ⅱ）用X表示甲、乙两人中在允许的时间内能赶到火车站的人数，针对（Ⅰ）的选择方案，求X的分布列和数学期望．
如图，从点P1（0，0）做x轴的垂线交曲线y=ex于点Q1（0，1），曲线在Q1点处的切线与x轴交于点P2，再从P2做x轴的垂线交曲线于点Q2，依次重复上述过程得到一系列点：P1，Q1；P2，Q2…；Pn，Qn，记Pk点的坐标为（xk，0）（k=1，2，…，n）．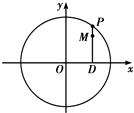
如图，设P是圆x2+y2=25上的动点，点D是P在x轴上的射影，M为PD上一点，且|MD|=
