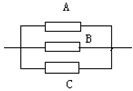
 如图,A,B,C表示3种开关,设在某段时间内它们正常工作的概率是分别是0.9,0.8,0.7,如果系统中至少有1个开关能正常工作,那么该系统正常工作的概率是( )
如图,A,B,C表示3种开关,设在某段时间内它们正常工作的概率是分别是0.9,0.8,0.7,如果系统中至少有1个开关能正常工作,那么该系统正常工作的概率是( )| A、0.504 | B、0.496 | C、0.994 | D、0.06 |
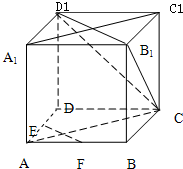 如图,正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点
如图,正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点(1)求证:EF∥平面CB1D1
(2)求证:平面CAA1C1⊥平面CB1D1
(3)设二面角B-B1D1-C 的大小为θ,求tanθ.
 如图,A,B,C表示3种开关,设在某段时间内它们正常工作的概率是分别是0.9,0.8,0.7,如果系统中至少有1个开关能正常工作,那么该系统正常工作的概率是( )
如图,A,B,C表示3种开关,设在某段时间内它们正常工作的概率是分别是0.9,0.8,0.7,如果系统中至少有1个开关能正常工作,那么该系统正常工作的概率是( )| A、0.504 | B、0.496 | C、0.994 | D、0.06 |
 如图,正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点
如图,正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点