关于平面向量
,
,
,有下列命题:
①(
•
)
-(
•
)
=0
②|
|-|
|<|
-
|;
③(
•
)
-(
•
)
不与
垂直;
④非零向量
和
满足|
|=|
|=|
-
|,则
与
-
的夹角为60°.
其中真命题的个数为( )
| a |
| b |
| c |
①(
| a |
| b |
| c |
| c |
| a |
| b |
②|
| a |
| b |
| a |
| b |
③(
| b |
| c |
| a |
| c |
| a |
| b |
| c |
④非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
其中真命题的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知a为实数,
>
,则a=( )
| 1+2i |
| a+i |
| 3 |
| 2 |
| A、.1 | ||
B、
| ||
C、.
| ||
| D、.-2 |
某班主任对全班50名学生学习积极性和对待班级工作的态度进行调查,统计数据如下表所示:
(I)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(II)试运用独立性检验的思想方法分析:是否有99%的把握认为学生的学习积极性与对待班级工作的态度有关系?并说明理由.P(K2≥k0)0.050.0250.0100.0050.001k03.8415.0246.6357.87910.828
参考公式及数据:K2=
.
0 31275 31283 31289 31293 31299 31301 31305 31311 31313 31319 31325 31329 31331 31335 31341 31343 31349 31353 31355 31359 31361 31365 31367 31369 31370 31371 31373 31374 31375 31377 31379 31383 31385 31389 31391 31395 31401 31403 31409 31413 31415 31419 31425 31431 31433 31439 31443 31445 31451 31455 31461 31469 266669
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(II)试运用独立性检验的思想方法分析:是否有99%的把握认为学生的学习积极性与对待班级工作的态度有关系?并说明理由.P(K2≥k0)0.050.0250.0100.0050.001k03.8415.0246.6357.87910.828
参考公式及数据:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
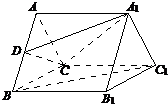 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=CA=AA1,D为AB的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=CA=AA1,D为AB的中点. 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7. 19、从某学校高三年级共800名男生中随机抽取50人测量身高.据测量被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图所示是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
19、从某学校高三年级共800名男生中随机抽取50人测量身高.据测量被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图所示是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.