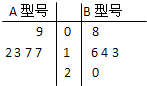
 某工厂生产A、B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品.为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:
某工厂生产A、B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品.为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:(1)试根据茎叶图所提供的数据,分别计算A、B两种产品为一等品的概率PA、PB;
(2)已知每件产品的利润如表一所示,用ξ、η分别表示一件A、B型产品的利润,在(1)的条件下,求ξ、η的分布列及数学期望(均值)Eξ、Eη;
(3)已知生产一件产品所需用的配件数和成本资金如表二所示,该厂有配件30件,可用资金40万元,设x、y分别表示生产A、B两种产品的数量,在(2)的条件下,求x、y为何值时,z=xEξ+yEη最大?最大值是多少?(解答时须给出图示)
表一
| 等级 利润 产品 |
一等品 | 二等品 |
| A型 | 4(万元) | 3(万元) |
| B型 | 3(万元) | 2(万元) |
| 项目 用量 产品 |
配件(件) | 资金(万元) |
| A型 | 6 | 4 |
| B型 | 2 | 8 |
对于任意实数a、b,当b>0时,定义运算a*b=
,则满足方程2*x=(-2)*x的实数x所在的区间为( )
|
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
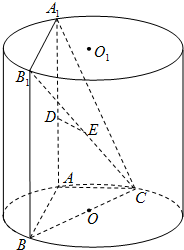 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥面CBB1.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥面CBB1.
 7、如图,在一个正方体内放入两个半径不相等的球O1、O2,这两个球相外切,且球O1与正方体共顶点A的三个面相切,球O2与正方体共顶点B1的三个面相切,则两球在正方体的面AA1C1C上的正投影是( )
7、如图,在一个正方体内放入两个半径不相等的球O1、O2,这两个球相外切,且球O1与正方体共顶点A的三个面相切,球O2与正方体共顶点B1的三个面相切,则两球在正方体的面AA1C1C上的正投影是( )