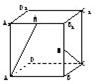
 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别为A1B1和BB1的中点,那么直线AM与CN所成的角为( )
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别为A1B1和BB1的中点,那么直线AM与CN所成的角为( )A、arccos
| ||||
B、arccos
| ||||
C、arccos
| ||||
D、arccos
|
函数f(x)=
的零点有( )
| (x-1)lnx |
| x-3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别为A1B1和BB1的中点,那么直线AM与CN所成的角为( )
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别为A1B1和BB1的中点,那么直线AM与CN所成的角为( )A、arccos
| ||||
B、arccos
| ||||
C、arccos
| ||||
D、arccos
|
| (x-1)lnx |
| x-3 |
| A、0个 | B、1个 | C、2个 | D、3个 |