具有性质:f(
)=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数中满足“倒负”变换的函数是( )
①y=x-
,②y=x+
,③y=
| 1 |
| x |
①y=x-
| 1 |
| x |
| 1 |
| x |
|
| A、①② | B、②③ | C、①③ | D、只有① |
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界、若函数f(x)=1+a•(
)x+(
)x在[0,+∞)上是以3为上界的有界函数,则实数a的取值范围是( )
| 1 |
| 2 |
| 1 |
| 4 |
| A、[-5,0] |
| B、[-4,1] |
| C、[-4,0] |
| D、[-5,1] |
设a>1,函数y=|logax|的定义域为[m,n](m<n),值域为[0,1],定义“区间[m,n]的长度等于n-m”,若区间[m,n]长度的最小值为
,则实数a的值内( )
| 5 |
| 6 |
| A、11 | ||
| B、6 | ||
C、
| ||
D、
|
函数f(x)=(
)x与函数g(x)=log
|x|在区间(-∞,0)上的单调性为( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、都是增函数 |
| B、都是减函数 |
| C、f(x)是增函数,g(x)是减函数 |
| D、f(x)是减函数,g(x)是增函数 |
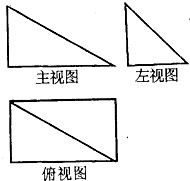 已知四棱锥P-ABCD的三视图如右图,该棱锥中,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在棱BC上移动.
已知四棱锥P-ABCD的三视图如右图,该棱锥中,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在棱BC上移动.