设f(n)=2n+1(n∈N),P={1,2,3,4,5},Q={3,4,5,6,7},记
={n∈N|f(n)∈P},
={n∈N|f(n)∈Q},则(
∩CN
)∪(
∩CN
)=( )
| ? |
| P |
| ? |
| Q |
| ? |
| P |
| ? |
| Q |
| ? |
| Q |
| ? |
| P |
| A、{0,3} |
| B、{1,2} |
| C、{3,4,5} |
| D、{1,2,6,7} |
已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是( )
| A、1 | B、-1 | C、2k+1 | D、-2k+1 |
在(1-x)5+(1-x)6+(1-x)7+(1-x)8的展开式中,含x3的项的系数是( )
| A、74 | B、121 | C、-74 | D、-121 |

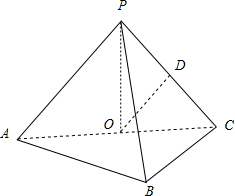 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.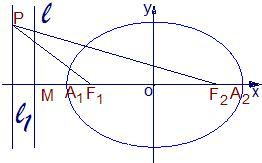 如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.