半径为R的球O的直径AB垂直于平面a,垂足为B,△BCD是平面a内边长为R的正三角形,线段AC、AD分别与球面交于点M、N,那么M、N两点间的球面距离是( )


A、Rarccos
| ||
B、Rarccos
| ||
C、
| ||
D、
|
已知正四棱锥S-ABCD中,SA=2
,那么当该棱锥的体积最大时,它的高为( )
| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为( )
| A、πa2 | ||
B、
| ||
C、
| ||
| D、5πa2 |
 在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,则斜截圆柱的侧面面积S=
在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,则斜截圆柱的侧面面积S=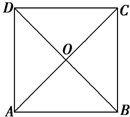 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为 长方体ABCD-A1B1C1D1的顶点均在同一个球面上,AB=AA1=1,BC=
长方体ABCD-A1B1C1D1的顶点均在同一个球面上,AB=AA1=1,BC=