题目内容
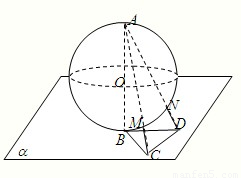
半径为R的球O的直径AB垂直于平面a,垂足为B,△BCD是平面a内边长为R的正三角形,线段AC、AD分别与球面交于点M、N,那么M、N两点间的球面距离是( )


A、Rarccos
| ||
B、Rarccos
| ||
C、
| ||
D、
|
分析:求解本题需要根据题意求解出题目中的角MON的余弦,再代入求解,即可求出MN的两点距离.
解答: 解:由已知,AB=2R,BC=R,
解:由已知,AB=2R,BC=R,
故tan∠BAC=
cos∠BAC=
连接OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=
R,
同理AN=
R,且MN∥CD
而AC=
R,CD=R
故MN:CD=AM:AC
MN=
R,
连接OM、ON,有OM=ON=R
于是cos∠MON=
=
所以M、N两点间的球面距离是Rarccos
.
故选A.
 解:由已知,AB=2R,BC=R,
解:由已知,AB=2R,BC=R,故tan∠BAC=
| 1 |
| 2 |
cos∠BAC=
2
| ||
| 5 |
连接OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=
4
| ||
| 5 |
同理AN=
4
| ||
| 5 |
而AC=
| 5 |
故MN:CD=AM:AC
MN=
| 4 |
| 5 |
连接OM、ON,有OM=ON=R
于是cos∠MON=
| OM2+ON2-MN2 |
| 2OM•ON |
| 17 |
| 25 |
所以M、N两点间的球面距离是Rarccos
| 17 |
| 25 |
故选A.
点评:本题考查学生的空间想象能力,以及学生对球面上的点的距离求解,是中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
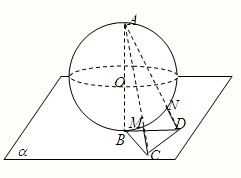 如图,半径为R的球O的直径AB垂直于平面α,垂足为B,△BCD是平面α内边长为R的正三角形,线段AC、AD分别与球面交于点M、N,那么M、N两点间的球面距离是
如图,半径为R的球O的直径AB垂直于平面α,垂足为B,△BCD是平面α内边长为R的正三角形,线段AC、AD分别与球面交于点M、N,那么M、N两点间的球面距离是