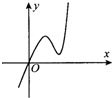
 定义在R上的函数f(x)满足f(4)=1.f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1.f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则| b+2 |
| a+2 |
A、(
| ||||
B、(-∞,
| ||||
C、(
| ||||
| D、(-∞,-3) |
 如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,则点A到直线l的距离AD为( )
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,则点A到直线l的距离AD为( )A、3
| ||||
B、
| ||||
C、
| ||||
D、
|
 定义在R上的函数f(x)满足f(4)=1.f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1.f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则| b+2 |
| a+2 |
A、(
| ||||
B、(-∞,
| ||||
C、(
| ||||
| D、(-∞,-3) |
 如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,则点A到直线l的距离AD为( )
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,则点A到直线l的距离AD为( )A、3
| ||||
B、
| ||||
C、
| ||||
D、
|