设
,
是一组非正交的基底,为得到正交基底,可在集合{
+t
|t∈R}中找一个向量与
组成一组正交基底,根据上述要求,若
=(1,2),
=(2,3),则t的值为( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
y=lnsin(-2x+
)的单调递减区间为( )
| π |
| 3 |
A、(kπ+
| ||||
B、(kπ+
| ||||
C、(kπ+
| ||||
D、[kπ-
|
已知α∈(0,π),cos(
-α)-cos(π-α)=
,则tanα的值为( )
| π |
| 2 |
| 17 |
| 25 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、
|
若非零平面向量
,
,
满足(
•
)•
=
•(
•
),则( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
要得到函数y=sin(2x+
)的图象,只需将函数y=cos2x的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
某扇形的半径为r,圆心角α所对的弧长为2r,则α的大小是( )
| A、30° | B、60° | C、1弧度 | D、2弧度 |
若A(1,-2,1),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
| A、不等边锐角三角形 | B、直角三角形 | C、钝角三角形 | D、等边三角形 |
已知向量
=(2,-1,3),
=(-4,2,x),使
⊥
成立的x与使
∥
成立的x分别为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、-6,
| ||
D、6,-
|


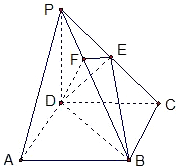 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.