已知f(x)为定义在(-∞,+∞)上的可导函数,且f(x)<f′(x)对于x∈R恒成立,则( )
| A、f(2)>e2f(0),f(2010)>e2010f(0) | B、f(2)<e2f(0),f(2010)>e2010f(0) | C、f(2)>e2f(0),f(2010)<e2010f(0) | D、f(2)<e2f(0),f(2010)<e2010f(0) |
已知函数f(x)=
,若f(x)在(-∞,+∞)上单调递增,则实数a的取值范围为( )
|
| A、(1,2) |
| B、(2,3) |
| C、(2,3] |
| D、(2,+∞) |
如图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图1;将线段AB围成一个圆,使两端点A、B恰好重合(从A到B是逆时针),如图2;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图3.图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.则下列说法中正确命题的是( )


A、f(
| ||
| B、f(x)是奇函数 | ||
| C、f(x)在定义域上单调递增 | ||
| D、f(x)的图象关于y轴对称 |
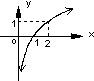 10、已知函数y=
10、已知函数y=
|
| A、2x | ||
B、log
| ||
| C、log2(-x) | ||
| D、-log2(-x) |
函数f(x)=
(x>1)的值域是( )
| 1 |
| x |
| A、(-∞,0)∪(0,+∞) |
| B、R |
| C、(1,+∞) |
| D、(0,1) |
若函数f(x)=logmx的反函数的图象过点(-1,n),则3n+m的最小值是( )
A、2
| ||
| B、2 | ||
C、2
| ||
D、
|
甲乙两人同时从A地出发往B地,甲在前一半时间以速度v1行驶,在后一半时间以速度v2行驶,乙在前一半路程以速度v1行驶,在后一半路程以速度v2行驶,(v1≠v2).则下列说法正确的是( )
| A、甲先到达B地 | B、乙先到达B地 | C、甲乙同时到达B地 | D、无法确定谁先到达B地 |
过曲线y=
(x>0)上横坐标为1的点的切线方程为( )
| x+1 |
| x2 |
| A、3x+y-1=0 |
| B、3x+y-5=0 |
| C、x-y+1=0 |
| D、x-y-1=0 |