定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则( )
A、f(sin
| ||||
| B、f(sin1)>f(cos1) | ||||
C、f(cos
| ||||
| D、f(cos2)>f(sin2) |
设O为坐标原点,点M(x,y)满足
,则z=2x+y的最大值为 ( )
|
| A、15 | B、5 | C、3 | D、-3 |
对于非零向量
,
,定义运算“#”:
#
=|
|•|
|sinθ,其中θ为
,
的夹角.有两两不共线的三个向量
,
,
,下列结论:
①若
#
=
#
,则
=
;②
#
=
#
;
③若
#
=0,则
∥
;④(
+
)#
=
#
+
#
;
⑤
#
=(-
)#
.
其中正确的个数有( )
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| a |
| b |
| c |
①若
| a |
| b |
| a |
| c |
| b |
| c |
| a |
| b |
| b |
| a |
③若
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
⑤
| a |
| b |
| a |
| b |
其中正确的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
过点A(a,a)可作圆x2+y2-2ax+a2+2a-3=0的两条切线,则实数a的取值范围为( )
A、a<-3或1<a<
| ||
B、1<a<
| ||
| C、a<-3 | ||
D、-3<a<1或a>
|
若(2x+
)n的展开式中,二项式系数最大的项只有第三项,则展开式中常数项的值为( )
| 1 |
| x |
| A、12 | B、18 | C、24 | D、32 |
已知某程序框图如图所示,则该程序运行后输出的结果为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中是假命题的是( )
| A、?m∈R,使f(x)=(m-1)•xm2-4m+3是幂函数,且在(0,+∞)上递减 | B、?a>0,函数f(x)=ln2x+lnx-a有零点 | C、?α,β∈R,使cos(α+β)=cosα+sinβ | D、?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 |
已知函数f(x)=Asin(ωx+α)的图象如图所示,f(
=-
,则f(0)=( )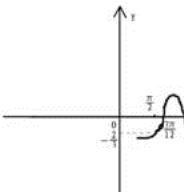
| π |
| 2 |
| 2 |
| 3 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|
