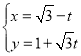(1)求函数g(x)的定义域；

(2)若f(x)是奇函数，且在定义域上单调递减，求不等式g(x)≤0的解集．

【题目】高中生在被问及“家，朋友聚集的地方，个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时，从洛阳的高中生中，随机抽取了55人，从上海的高中生中随机抽取了45人进行答题.洛阳高中生答题情况是：选择家的占、选择朋友聚集的地方的占、选择个人空间的占.上海高中生答题情况是：选择朋友聚集的地方的占、选择家的占、选择个人空间的占.

（1）请根据以上调查结果将下面列联表补充完整，并判断能否有的把握认为“恋家（在家里感到最幸福）”与城市有关：

（2） 从被调查的不“恋家”的上海学生中，用分层抽样的方法选出4人接受进一步调查，从被选出的4 人中随机抽取2人到洛阳交流学习，求这2人中含有在“个人空间”感到幸福的学生的概率.

附：，其中d.

【题目】铁人中学高二学年某学生对其亲属30人饮食习惯进行了一次调查，并用如图所示的茎叶图表示30人的饮食指数．（说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主．）

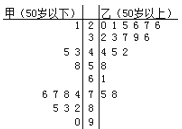
（Ⅰ）根据茎叶图，帮助这位学生说明其亲属30人的饮食习惯；

（Ⅱ）根据以上数据完成下列的列联表：

（Ⅲ）能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系？

附：.

【题目】在平面直角坐标系中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，两种坐标系中取相同的长度单位.已知直线l的参数方程为（t为参数），曲线C的极坐标方程为ρ＝4sin（θ+）.

（1）求直线l的普通方程与曲线C的直角坐标方程；

（2）若直线l与曲线C交于M，N两点，求△MON的面积.

【题目】（本小题满分12分）已知椭圆的离心率为，椭圆的短轴端点与双曲线的焦点重合，过点且不垂直于轴的直线与椭圆相交于两点.

（1）求椭圆的方程；

（2）求的取值范围.

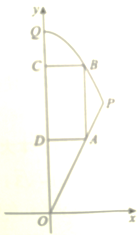
【题目】如图，曲边三角形中，线段是直线的一部分，曲线段是抛物线的一部分.矩形的顶点分别在线段，曲线段和轴上.设点，记矩形的面积为.

（Ⅰ）求函数的解析式并指明定义域；

（Ⅱ）求函数的最大值.

【答案】(Ⅰ) 定义域为;(Ⅱ) 在时，取得最大值.

【解析】试题分析：( I )根据点在直线上，在抛物线上，结合图形，可得点，从而可得函数的解析式，联立直线与抛物线的方程，即可求得定义域；（II）对函数求导，利用导数研究函数的单调性，从而可求得函数的最大值.

试题解析：( I )令，

解得 （舍）

因为点

所以 ，

其定义域为

（II）因为

令，得，（舍）

所以的变化情况如下表

因为是函数在上的唯一的一个极大值，

所以在时，函数取得最大值.

点睛：利用导数解答函数最值的一般步骤：第一步：利用或求单调区间；第二步：解得两个根；第三步：比较两根同区间端点的大小；第四步：求极值；第五步：比较极值同端点值的大小．

【题型】解答题
【结束】
16

【题目】在各项均为正数的数列中， 且.

（Ⅰ）当时，求的值；

（Ⅱ）求证：当时，.

为了研究计算的方便，工作人员将上表的数据进行了处理， 得到下表2：

（Ⅰ）求z关于t的线性回归方程；

（Ⅱ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？

（附：对于线性回归方程，其中）

【题目】已知抛物线的焦点为，为抛物线上异于原点的任意一点，过点的直线交抛物线于另一点，交轴的正半轴于点，且有.当点的横坐标为3时，为正三角形.

（1）求抛物线的方程；

（2）若直线，且和抛物线有且只有一个公共点，试问直线是否过定点，若过定点，求出定点坐标；若不过定点，请说明理由.

【题目】设函数.

（1）已知函数,求的极值；

（2）已知函数,若存在实数,使得当时,函数的最大值为,求实数的取值范围.

【题目】已知函数，其中.

（1）函数的图象能否与轴相切?若能，求出实数，若不能，请说明理由；

（2）讨论函数的单调性.