【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
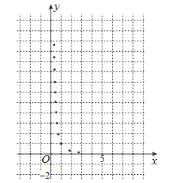
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为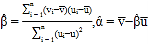 .
.
【题目】某中学为调查该校学生每周参加社会实践活动的情况,随机收集了若干名学生每周参加社会实践活动的时间(单位:小时),将样本数据绘制如图所示的频率分布直方图,且在[0,2)内的学生有1人.
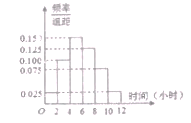
(1)求样本容量![]() ,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
(2)将每周参加社会实践活动时间在[4,12]内定义为“经常参加社会实践”,参加活动时间在[0,4)内定义为“不经常参加社会实践”.已知样本中所有学生都参加了青少年科技创新大赛,有13人成绩等级为“优秀”,其余成绩为“一般”,其中成绩优秀的13人种“经常参加社会实践活动”的有12人.请将2×2列联表补充完整,并判断能否在犯错误的概率不超过0.05的前提下认为青少年科技创新大赛成绩“优秀”与经常参加社会实践活动有关;
(3)在(2)的条件下,如果从样本中“不经常参加社会实践”的学生中随机选取两人参加学校的科技创新班,求其中恰好一人成绩优秀的概率.
参考公式和数据:
![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |