【题目】2017年5月,“一带一路”沿线的20国青年评选出了中国“新四大发明”:高铁、支付宝、共享单车和网购.2017年末,“支付宝大行动”用发红包的方法刺激支付宝的使用.某商家统计前5名顾客扫描红包所得金额分别为5.5元,2.1元,3.3元,5.9元,4.7元,商家从这5名顾客中随机抽取3人赠送台历.
(1)求获得台历是三人中至少有一人的红包超过5元的概率;
(2)统计一周内每天使用支付宝付款的人数![]() 与商家每天的净利润
与商家每天的净利润![]() 元,得到7组数据,如表所示,并作出了散点图.
元,得到7组数据,如表所示,并作出了散点图.

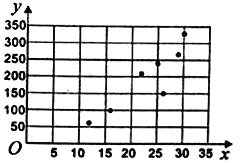
(i)直接根据散点图判断,![]() 与
与![]() 哪一个适合作为每天的净利润的回归方程类型.(
哪一个适合作为每天的净利润的回归方程类型.(![]() 的值取整数)
的值取整数)
(ii)根据(i)的判断,建立![]() 关于
关于![]() 的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
参考数据:
|
|
|
|
22.86 | 194.29 | 268.86 | 3484.29 |
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为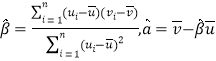 .
.
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)若将频率视为概率,现再从该校一年级全体学生中,采用随机抽样的方法每次抽取1名学生,抽取5次,记被抽取的5名学生中对冰球有兴趣的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,期望和方差.
的分布列,期望和方差.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
