10.关于z的方程z+i=2+iz的根是( )
| A. | $\frac{3}{2}-\frac{1}{2}$i | B. | $\frac{3}{2}+\frac{1}{2}$i | C. | 3-i | D. | 3+i |
7.某品牌电视专卖店,在“五一”期间设计一项有奖促销活动:每购买一台电视,即可通过电脑产生一组3个数的随机数组,根据下表兑奖:
商家为了了解计划的可行性,估计奖金数,进行了随机模拟试验,产生20组随机数组,每组3个数,试验结果如下所示:
975,146,858,513,277,645,903,756,111,783,
834,527,060,089,221,368,054,669,863,175.
(Ⅰ)请根据以上模拟数据估计:若活动期间商家卖出100台电视应付出奖金多少元?
(Ⅱ)在以上模拟数据的前5组数中,随机抽取2组数,试写出所有的基本事件,并求至少有一组获奖的概率.
| 随机数组的特征 | 3个数字均相同 | 恰有2个数字相同 | 其余情况 |
| 奖金(单位:元) | 500 | 200 | 0 |
975,146,858,513,277,645,903,756,111,783,
834,527,060,089,221,368,054,669,863,175.
(Ⅰ)请根据以上模拟数据估计:若活动期间商家卖出100台电视应付出奖金多少元?
(Ⅱ)在以上模拟数据的前5组数中,随机抽取2组数,试写出所有的基本事件,并求至少有一组获奖的概率.
6.已知点P,Q为圆C:x2+y2=25上的任意两点,且|PQ|<6,若PQ中点组成的区域为M,在圆C内任取一点,则该点落在区域M(2,-1)上的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{9}{25}$ | C. | $\frac{16}{25}$ | D. | $\frac{2}{5}$ |
4.已知直线$\sqrt{m}$x+$\sqrt{n}$y=4被圆x2+y2=25截得的弦长为6,则直线mx+ny=4与圆(x-1)2+(y-2)2=20的位置关系是( )
0 250469 250477 250483 250487 250493 250495 250499 250505 250507 250513 250519 250523 250525 250529 250535 250537 250543 250547 250549 250553 250555 250559 250561 250563 250564 250565 250567 250568 250569 250571 250573 250577 250579 250583 250585 250589 250595 250597 250603 250607 250609 250613 250619 250625 250627 250633 250637 250639 250645 250649 250655 250663 266669
| A. | 相离 | B. | 相切 | ||
| C. | 相交且有可能过圆心 | D. | 相交但不过圆心 |
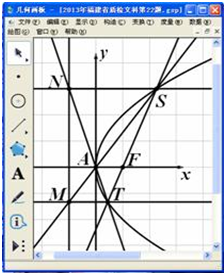 某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.
某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.