13.不等式ax2+4x+a<1+x2对一切x∈R恒成立,则实数a的取值范围是( )
| A. | (3,+∞) | B. | (-∞,-1) | C. | (-∞,1) | D. | (-∞,-1)∪(3,+∞) |
12.下列说法不正确的是( )
| A. | 命题“?x∈R,x2≥0”的否定为“?x0∈R,x2<0” | |
| B. | “a>b”是“ac2>bc2”的必要不充分条件 | |
| C. | “若x2-6x+5≠0,则x≠1”是真命题 | |
| D. | 命题p:A成立,命题q:B成立,则命题¬p∨¬q表示A,B至少有一个成立 |
10.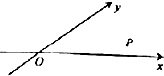 如图,a∈(0,π),且a≠$\frac{π}{2}$,当∠xOy=e时,定义平面坐标系xOy为a仿射坐标系,在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y),若在仿射坐标系中,已知$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(s,t),下列结论中不正确的是( )
如图,a∈(0,π),且a≠$\frac{π}{2}$,当∠xOy=e时,定义平面坐标系xOy为a仿射坐标系,在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y),若在仿射坐标系中,已知$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(s,t),下列结论中不正确的是( )
 如图,a∈(0,π),且a≠$\frac{π}{2}$,当∠xOy=e时,定义平面坐标系xOy为a仿射坐标系,在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y),若在仿射坐标系中,已知$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(s,t),下列结论中不正确的是( )
如图,a∈(0,π),且a≠$\frac{π}{2}$,当∠xOy=e时,定义平面坐标系xOy为a仿射坐标系,在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y),若在仿射坐标系中,已知$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(s,t),下列结论中不正确的是( )| A. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,则m=s,n=t | |
| B. | 若$\overrightarrow{a}$$∥\overrightarrow{b}$,则mt-ns=0 | |
| C. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则ms+nt=0 | |
| D. | 若m=t=1,n=s=2,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角$\frac{π}{3}$,则a=$\frac{2π}{3}$ |
9.在某次测量中,得到的A样本数据为81,82,82,84,84,85,86,86,86,若B样本数据恰好是A样本数据分别加2后所得的数据,则A、B两个样本的下列数字特征对应相同的是( )
| A. | 众数 | B. | 平均数 | C. | 标准差 | D. | 中位数 |
6.某班有50名学生,某次数学成绩经计算后得到的平均数是65分,标准差是s,后来发现记录有误,甲得65分却记为56分,乙得45分误记为54分,更正后重新计算,标准差为s1,则s与s1之间的大小关系是( )
| A. | s═s1 | B. | s>s1 | C. | s<s1 | D. | 不能确定 |
5.某高级中学采用系统抽样的方法从全体1260名学生中抽取60名学生做视力健康检查,现将1260名学生从1~1260进行编号,若在抽取的样本中有一个编号为355,则样本中最小的编号是( )
0 250397 250405 250411 250415 250421 250423 250427 250433 250435 250441 250447 250451 250453 250457 250463 250465 250471 250475 250477 250481 250483 250487 250489 250491 250492 250493 250495 250496 250497 250499 250501 250505 250507 250511 250513 250517 250523 250525 250531 250535 250537 250541 250547 250553 250555 250561 250565 250567 250573 250577 250583 250591 266669
| A. | 19 | B. | 18 | C. | 17 | D. | 16 |
 设函数f(x)=Asin(ωx+φ),(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(100)=2+2$\sqrt{2}$.
设函数f(x)=Asin(ωx+φ),(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(100)=2+2$\sqrt{2}$.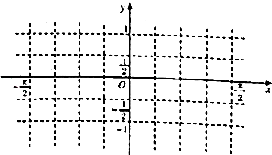 已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为π.
已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为π.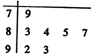 七位评委为某跳水运动员打出的分数的茎叶图如图,其极差为14.
七位评委为某跳水运动员打出的分数的茎叶图如图,其极差为14.