12.己知全集U=R,函数y=$\frac{1}{\sqrt{x+2}}$的定义域为集合A,函数y=log3(x+1)的定义域为B,则集合A∩(∁UB)=( )
| A. | (2,-1) | B. | (-2,-1] | C. | (-∞,-2) | D. | [-1,+∞) |
11.已知抛物线y2=8x焦点与双曲线$\frac{x^2}{a^2}-{y^2}=1$(a>0)的右焦点重合,则此双曲线的离心率是( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
10.设命题p:实数x,y满足$\left\{\begin{array}{l}{4x+3y-12≥0}\\{x-t≤0}\\{x+3y≤12}\end{array}\right.$,(t>0);命题q:实数x,y满足(x-3)2+y2≤25(x,y∈R),若p是q的充分不必要条件,则t的取值范围是为( )
| A. | (0,3] | B. | (0,5] | C. | (0,6] | D. | (1,6] |
8.设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[a-1,a+1],关于x 的不等式f(x2+a)>a2f(x)恒成立,则实数a的取值范围是( )
| A. | (0,2] | B. | (0,4] | C. | (0,+∞) | D. | [2,+∞) |
7.在锐角△ABC中,tanA=t+1,tanB=t-1,则实数t的取值范围是( )
0 249847 249855 249861 249865 249871 249873 249877 249883 249885 249891 249897 249901 249903 249907 249913 249915 249921 249925 249927 249931 249933 249937 249939 249941 249942 249943 249945 249946 249947 249949 249951 249955 249957 249961 249963 249967 249973 249975 249981 249985 249987 249991 249997 250003 250005 250011 250015 250017 250023 250027 250033 250041 266669
| A. | ($\sqrt{2}$,+∞) | B. | (1,+∞) | C. | (1,$\sqrt{2}$) | D. | (-1,1) |
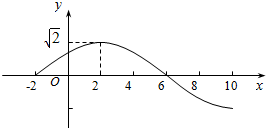 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示.