8.${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$(cos$\frac{x}{2}$-sin$\frac{x}{2}$)2dx=( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
7.函数y=ln(x+1)与y=$\frac{a}{x}$的图象的一个交点的横坐标所在区间为(1,2),则实数a的取值范围是( )
| A. | (-∞,2ln3) | B. | (ln2,2ln3) | C. | (ln2,+∞) | D. | (-∞,2ln3)∪(ln2,+∞) |
3.若2sin2x=cos2x+1,且cosx≠0,则tan2x=( )
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{17}$ |
2.某单位有2000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如表所示:
(1)若要抽取40人调查身体状况,则应怎样抽样?
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
(3)若要抽取20人调查对广州亚运会举办情况的了解,则应怎样抽样?
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
(3)若要抽取20人调查对广州亚运会举办情况的了解,则应怎样抽样?
1.函数y=$\frac{{x}^{2}+2x+6}{x-1}$(x>1)的最小值为( )
| A. | 10 | B. | 9 | C. | 6 | D. | 4 |
20.将函数f(x)=2sin(3x+$\frac{π}{4}$)的图象向左平移$\frac{π}{3}$个单位后得到函数y=g(x)的图象,则函数y=f(x)与函数y=g(x)的图象关于( )
0 249692 249700 249706 249710 249716 249718 249722 249728 249730 249736 249742 249746 249748 249752 249758 249760 249766 249770 249772 249776 249778 249782 249784 249786 249787 249788 249790 249791 249792 249794 249796 249800 249802 249806 249808 249812 249818 249820 249826 249830 249832 249836 249842 249848 249850 249856 249860 249862 249868 249872 249878 249886 266669
| A. | x轴对称 | B. | 原点对称 | C. | y轴对称 | D. | 直线x=$\frac{π}{2}$对称 |
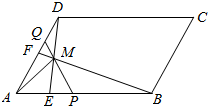 如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.