5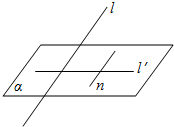．如图.设直线l是平面α的一条射线.l′是l在α内的射影.直线n?α．用＜a.b＞表示直线a.b的夹角．求证:(1)cos＜l.n＞=cos＜l.l′＞•cos＜l′.n＞,(2)n⊥l——青夏教育精英家教网——

如图，设直线l是平面α的一条射线，l′是l在α内的射影，直线n?α．用＜a，b＞表示直线a，b的夹角．求证：
（1）cos＜l，n＞=cos＜l，l′＞•cos＜l′，n＞；
（2）n⊥l?n⊥l′．

4．已知函数f（x）=2^x+x，g（x）=x-log${\;}_{\frac{1}{2}}$x，h（x）=log₂x-$\sqrt{x}$的零点分别为x₁，x₂，x₃，则x₁，x₂，x₃的大小关系是x₁＜x₂＜x₃．

3．用数学归纳法证明：1+2+2²+2³+…+2ⁿ⁺¹=2ⁿ⁺²-1，在验证n=1时，左端计算所得的项为（　　）

2．设函数f（x）=ln（1+x），g（x）=xf′（x）（x≥0），其中f′（x）是f（x）的导函数．
（1）若a≤1，求证：f（x）≥ag（x）．
（2）若g₁（x）=g（x），g_n+1（x）=g（g_n（x）），n∈N₊，求g₁（x），g₂（x），g₃（x）解析式，猜想g_n（x）的解析式，并用数学归纳法证明．

1．比较2ⁿ与2n+1的大小并证明．

20．是否存在常数a，b，使等式$\frac{{1}^{2}}{1×3}$+$\frac{{2}^{2}}{3×5}$+…+$\frac{{n}^{2}}{（2n-1）（2n+1）}$=$\frac{a{n}^{2}+n}{bn+2}$对于一切n∈N^*都成立？若存在，用数学归纳法证明之，若不存在，说明理由．

19．如果事件A，B互斥，记$\overline{A}$，$\overline{B}$分别为事件A，B的对立事件，那么（　　）

A∪B是必然事件

$\overline{A}$∪$\overline{B}$是必然事件

$\overline{A}$与$\overline{B}$一定互斥

$\overline{A}$与$\overline{B}$一定不互斥

18．方程cos²x+cos²2x+cos²4x+cos²8x=$\sqrt{\frac{sin16x}{sinx}}$的解集是{x|x=2kπ，k∈Z}．

17．“抢红包”的网络游戏有多种玩法，小明在十八岁生日举行成人礼时参加一种接龙红包游戏；小明在红包里装了9元现金，然后发给好友甲，并给出金额所在区间[1，9]，让甲猜（所猜金额为整数元；下同），如果甲猜中，甲将获得红包里的金额；如果甲未猜中，甲和当前的红包转给好友乙，同时给出金额所在区间[6，9]，让乙猜，如果乙猜同，甲和乙可以平分红包里的金额；如果乙未猜中，乙要将当前的红包转发给好友丙，同时给出金额所在区间[8，9]，让丙猜，如果丙猜中，甲、乙和丙可以平分红包里的金额，如果丙未猜中，红包里的资金将退回小明的帐户．
（1）求丙得到的0元的概率；
（2）从概率统计的角度而言，甲所获得的金额是否超过乙和丙两人所获得的金额之和？说明理由．

16．使函数f（x）=sin（2x+θ）+$\sqrt{3}$cos（2x+θ）（其中0＜θ＜π）是奇函数，则θ的值是$\frac{2π}{3}$．

0 249623 249631 249637 249641 249647 249649 249653 249659 249661 249667 249673 249677 249679 249683 249689 249691 249697 249701 249703 249707 249709 249713 249715 249717 249718 249719 249721 249722 249723 249725 249727 249731 249733 249737 249739 249743 249749 249751 249757 249761 249763 249767 249773 249779 249781 249787 249791 249793 249799 249803 249809 249817 266669