16．给出下面类比推理:①由“若2a＜2b.则a＜b .可类比推出:“若a2＜b2.则a＜b ,②由“ .可类比推出“$\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$ ,——青夏教育精英家教网——

16．给出下面类比推理：（注：下列集合C为复数集）
①由“若2a＜2b，则a＜b”，可类比推出：“若a²＜b²，则a＜b”；
②由“（a+b）c=ac+bc（c≠0）”，可类比推出“$\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}（c≠0）$”；
③由“当a，b∈R，若a-b=0，则a=b”，可类比推出“当a，b∈C，若a-b=0，则a=b”；
④由“当a，b∈R，若a-b＞0，则a＞b”，可类比推出“当a，b∈C，若a-b＞0，则a＞b”．
其中结论正确的个数为（　　）

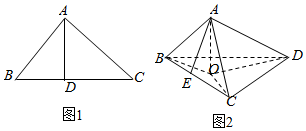如图1所示，在△ABC中，AB⊥AC，AD⊥BC，则AB²=BD•BC．类似有命题：在三棱锥A-BCD中，如图2所示，AD⊥面ABC．若A在△BCD内的射影为O，E在BC上，且E，O，D在同一条直线上，则S_△ABC²=S_△BCO•S_△BCD，此命题是（　　）

	A．	假命题
	B．	增加AB⊥AC的条件才是真命题
	C．	真命题
	D．	增加三棱锥A-BCD是正棱锥的条件才是真命题

14．设a₁，a₂，…，a_π均为正数，已知两个数的均值定理为：$\frac{{{a_1}+{a_2}}}{2}≥\sqrt{{a_1}•{a_2}}$．三个数的均值定理为：$\frac{{{a_1}+{a_2}+{a_3}}}{3}≥3\sqrt{{a_1}•{a_2}•{a_3}}$．据此写出n个数均值定理：$\frac{{a}_{1}{+a}_{2}{+a}_{3}+…{+a}_{n}}{n}$≥$\root{n}{{a}_{1}{•a}_{2}{•a}_{3}…{•a}_{n}}$．

13．a、b、c∈R，且a+b+c=0，abc＞0，则$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$的值（　　）

一定是负数

一定是正数

正负不能确定

12．设矩阵A=$[\begin{array}{l}{m}&{0}\\{0}&{n}\end{array}]$，若矩阵A的属于特征值1的一个特征向量为$[\begin{array}{l}{1}\\{0}\end{array}]$，属于特征值2的一个特征向量为$[\begin{array}{l}{0}\\{1}\end{array}]$，求矩阵A．

11．在等差数列{a_n}中，若a₁₂=0，则有a₁+a₂+…+a_n=a₁+a₂+…+a_23-n（n＜23，n∈N^*）成立，类比上述性质，在等比数列{b_n}中，若b₈=1，则有b₁•b₂…b_n=b₁•b₂…b_15-n（n＜15，且n∈N^*）成立．

10．我们用圆的性质类比球的性质如下：
①p：圆心与弦（非直径）中点的连线垂直于弦；q：球心与小圆截面圆心的连线垂直于截面．
②p：与圆心距离相等的两条弦长相等； q：与球心距离相等的两个截面圆的面积相等．
③p：圆的周长为C=πd（d是圆的直径）； q：球的表面积为S=πd²（d是球的直径）．
④p：圆的面积为S=$\frac{1}{2}$R•πd（R，d是圆的半径与直径）；q：球的体积为V=$\frac{1}{3}$R•πd²（R，d是球的半径与直径）．
则上面的四组命题中，其中类比得到的q是真命题的有（　　）个．

9．在平面直角坐标系xOy中，点A（-$\sqrt{2}$，1）关于原点O的对称点为点B，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率是$\frac{\sqrt{2}}{2}$，且过点B．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若点P是椭圆C上的异于点A，B的一动点，直线AP斜率为k₁，直线BP斜率为k₂，证明：k₁•k₂=-$\frac{1}{2}$；
（Ⅲ）是否存在直线l与椭圆C交于不同的两点M，N，使四边形OMBN为平行四边形，若存在，求出直线l的方程；若不存在，请说明理由．

如图所示，小圆圈表示网络的结点，结点之间的连线表示它们有网线相连，连线标注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点B向结点A传递信息，信息可以分开沿不同的路线同时传递，则一次性传递的最大信息量为（　　）

7．三角形的面积$s=\frac{1}{2}（a+b+c）r$，a﹑b﹑c 为三边的边长，r为三角形内切圆半径，利用类比推理可以得到四面体的体积为（　　）

	A．	V=$\frac{1}{3}$abc
	B．	$V=\frac{1}{3}sh$
	C．	$V=\frac{1}{3}（ab+bc+ca）h$
	D．	$V=\frac{1}{3}（{s_1}+{s_2}+{s_3}+{s_4}）r$（s₁，s₂，s₃，s₄分别为四个面的面积，r为四面体内切球半径）

0 241142 241150 241156 241160 241166 241168 241172 241178 241180 241186 241192 241196 241198 241202 241208 241210 241216 241220 241222 241226 241228 241232 241234 241236 241237 241238 241240 241241 241242 241244 241246 241250 241252 241256 241258 241262 241268 241270 241276 241280 241282 241286 241292 241298 241300 241306 241310 241312 241318 241322 241328 241336 266669